2DGS

https://arxiv.org/abs/2403.17888

https://surfsplatting.github.io/

Mesh生成器: 3D 高斯可能因为体积过大而模糊，深度不一致

Primitive

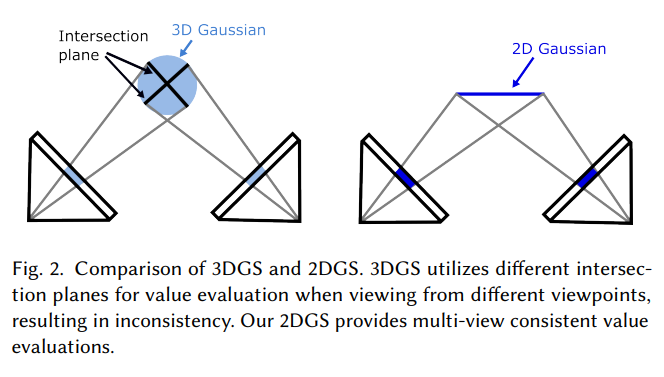
• Unlike 3DGS [Kerbl et al. 2023], which models the entire angular radiance in a blob, we simplify the 3-dimensional modeling by adopting “flat” 2D Gaussians embedded in 3D space.
• With 2D Gaussian modeling, the primitive distributes densities within a planar disk, defining the normal as the direction of the steepest change of density. (法线垂直于2D盘)
• By skipping the third row and column of \(\Sigma'\), we obtain a 2D Gaussian \(G_{2D}\) with covariance matrix \(\Sigma_{2D}\).

3D Space

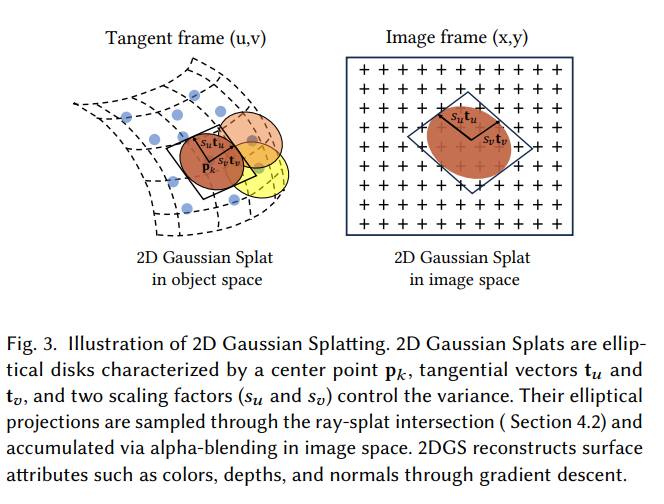
• Its central point is $p_k$,
• Two principal tangential vectors \(t_u\) and \(t_v\)
• A scaling vector \(S = (s_u, s_v)\) that controls the variances of the 2D Gaussian.
• The primitive normal: \(t_w = t_u \times t_v\).
• The orientation: \(3 \times 3\) rotation matrix \(R = [t_u, t_v, t_w]\),
• The scaling factors: \(3 \times 3\) diagonal matrix: \(S = \begin{bmatrix} s_u & 0 & 0 \\ 0 & s_v & 0 \\ 0 & 0 & 0 \end{bmatrix}\)
• P(u,v) : 平面上某个点在世界坐标系的位置

Splatting

\[x = (xz, yz, z, z)^{\top} = W P(u,v) = W H(u, v, 1, 1)^{\top}.\]

• x is ray emitted from the camera and passing through pixel (𝑥, 𝑦) and intersecting the splat at depth 𝑧.
• \(M = {(WH)}^{-1}\) : project its conic into the screen space with an implicit method
  • 普通仿射 → 只保证椭圆中心点在对的位置，边缘可能扭曲
  • implicit conic → 用一个方程描述整个椭圆在相机平面上的位置和形状，保证整体投影准确

问题：Inverse transformation introduces numerical instability

特别是当当 splat 从侧面看几乎退化成线时，逆矩阵求射线交点可能不是确定解（无数交点）

解决：Ray-splat Intersection

• 每个像素坐标 x=(x,y) 对应一个射线
• 将这个射线表示为两个正交平面的交线
• 平面变换到高斯局部坐标

• 求交点

问题：特殊pose

When a 2D Gaussian is observed from a slanted viewpoint, it degenerates to a line in screen space. Therefore, it might be missed during rasterization.

To deal with these cases and stabilize optimization

解决：Degenerate Solutions

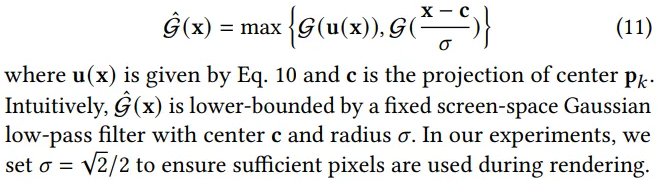
加一个 固定屏幕空间半径的低通高斯滤波 → 保证每个退化 splat 仍然有贡献 → 优化稳定

给贡献不突出的点强行加一点影响值, 以中心 c 为圆心，半径 σ 的高斯保底

这样 rasterization 不会漏掉 splat → 梯度稳定 → 可微分渲染可靠

Rasterization

没啥好说的

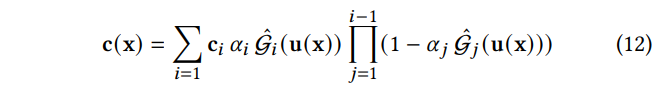
训练：额外加了两个Term

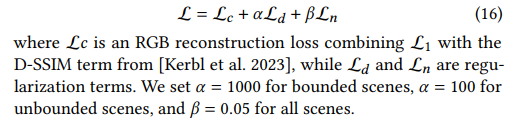
Normal Consistency

让每个 splat 的法向量和真实物体表面法向量 尽量一致

• \(n_i\) represents the normal of the splat that is oriented towards the camera
• 𝜔 denotes the blending weight of the intersection point
• N is the normal estimated by the gradient of the depth map
  • 沿射线累积透明度到 0.5 的点 作为表面点 $p_s$

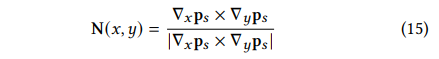
Depth Distortion

encourages the concentration of the splats

• concentrates 2D primitives distributed within a tight range along the ray, addressing the rendering process’s limitation where the distance between Gaussians is ignored.

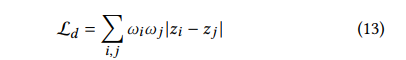
• \(𝜔\) denotes the blending weight of the intersection point
• \(𝑧_𝑖\) is the depth of the intersection points