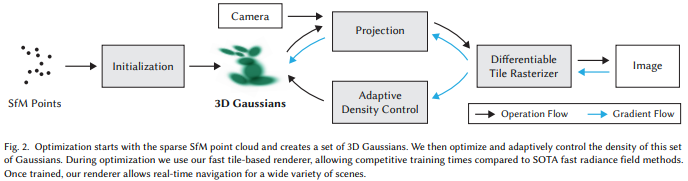
3DGS
3D 高斯椭球(捏雪球)
- 椭球是实心的
- 椭球的中心点: 3D高斯的均值 (x,y,z)
- 椭球的形状: 3D高斯的协方差矩阵 $\Sigma = RS S^T R^T$ (包含了旋转矩阵R 和 轴缩放矩阵S)
椭球的初始形状:
为了铺满画面 (simple-knn)
- 是—个球 (Sotropic Gaussian)
- 使用knn法,找到3近邻
- 半径是与3近邻的距离
投影矩阵(抛雪球)
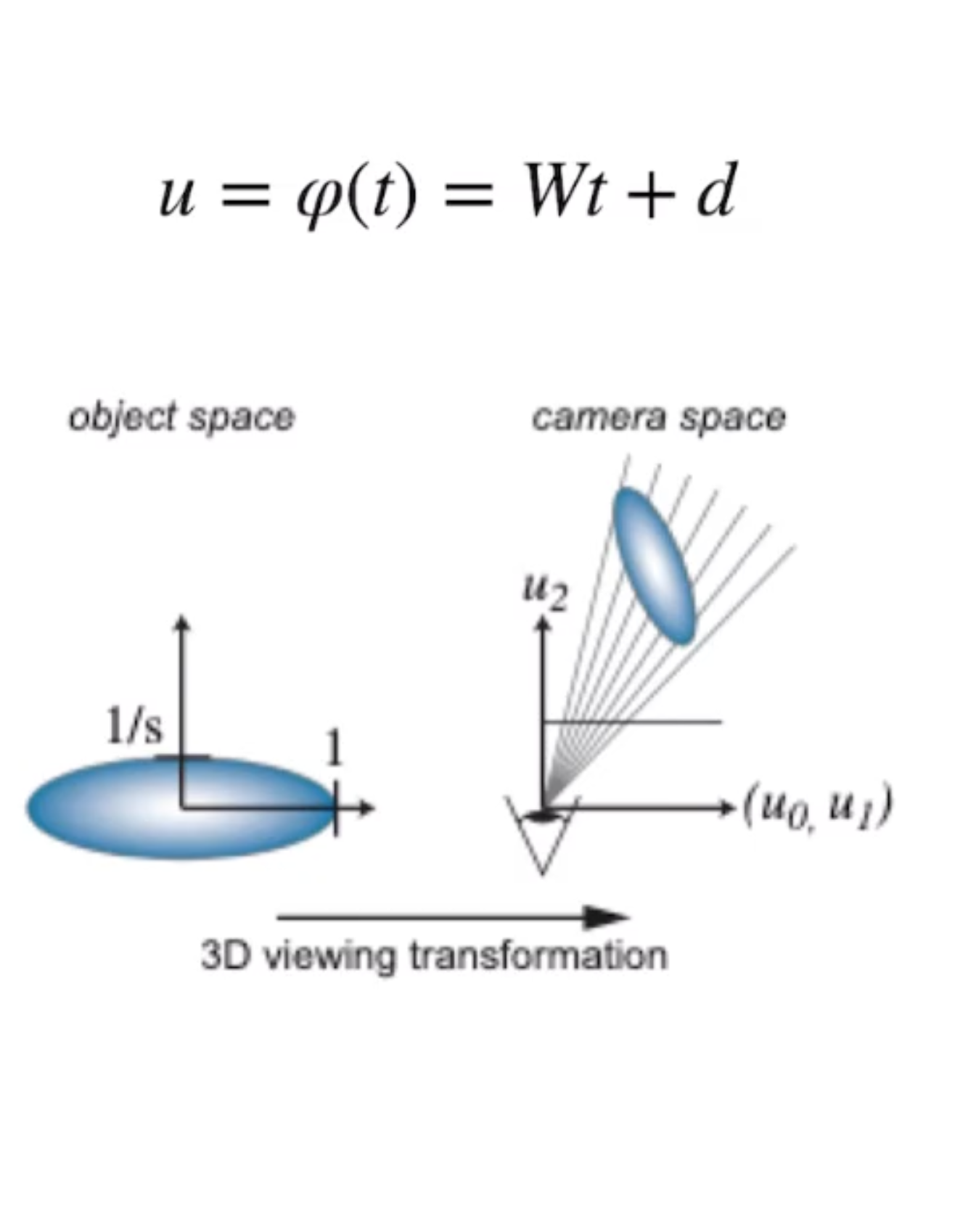
物理坐标系 → 相机坐标系:
- 均值变化 $u_k = Wt_k + d$
- 协方差矩阵变换 $\Sigma’ = W \Sigma W^T$
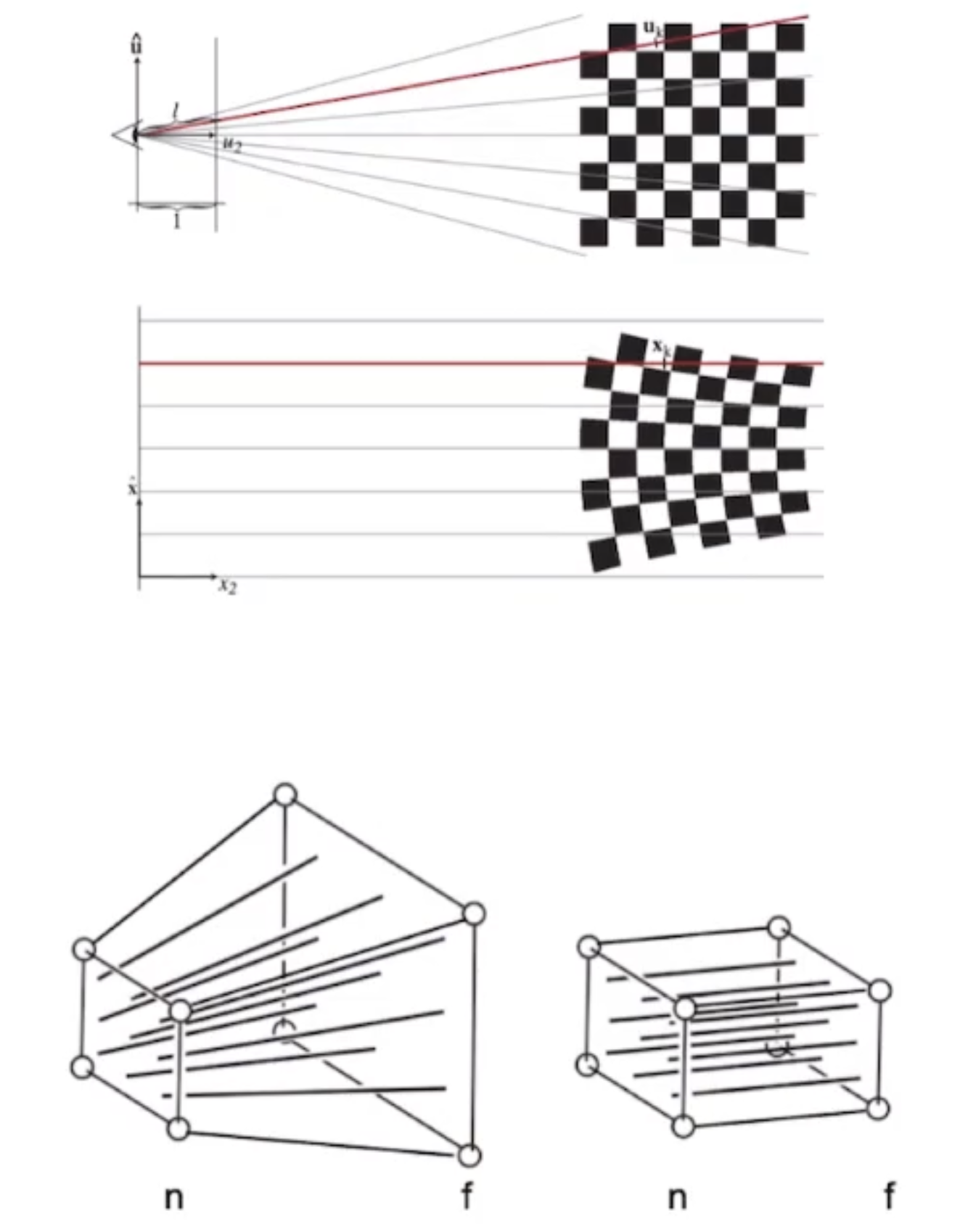
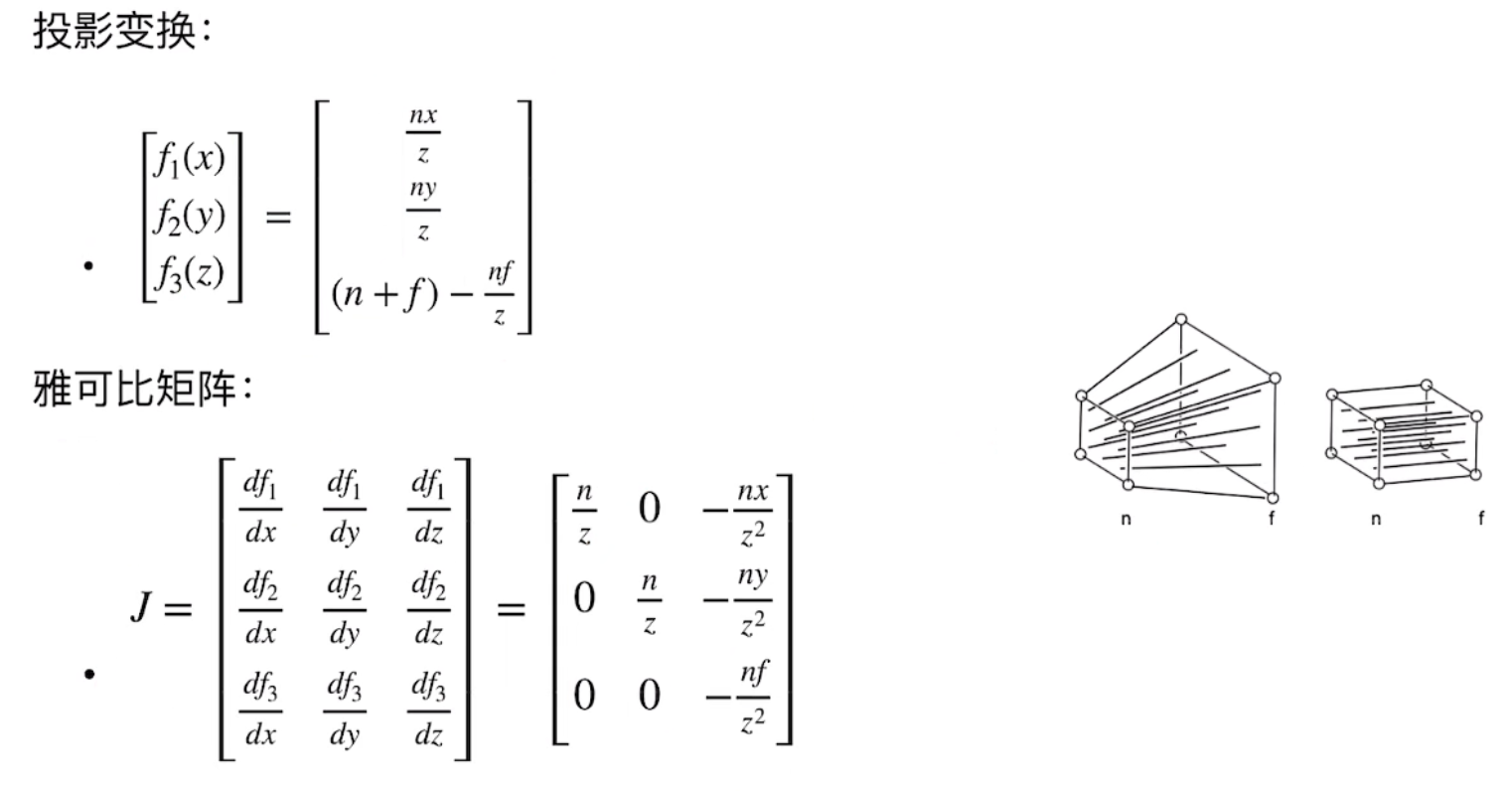
投影变换(非线性):
在高斯中心点附近,投影结果还算准确。但是在高斯的外围区域,透视投影效果会不准(perspective distortion 出现)。
$x = m(t)$
- 协方差变换是非线性变化, 所以需要雅可比矩阵进行 (模拟) 转化:: $\Sigma’ = JW \Sigma W^T J^T$
- J is the Jacobian of the affine approximation of the projective transformation
- W is the viewing transformation
- 均值可以直接应用: $x_k = m(u_k)$
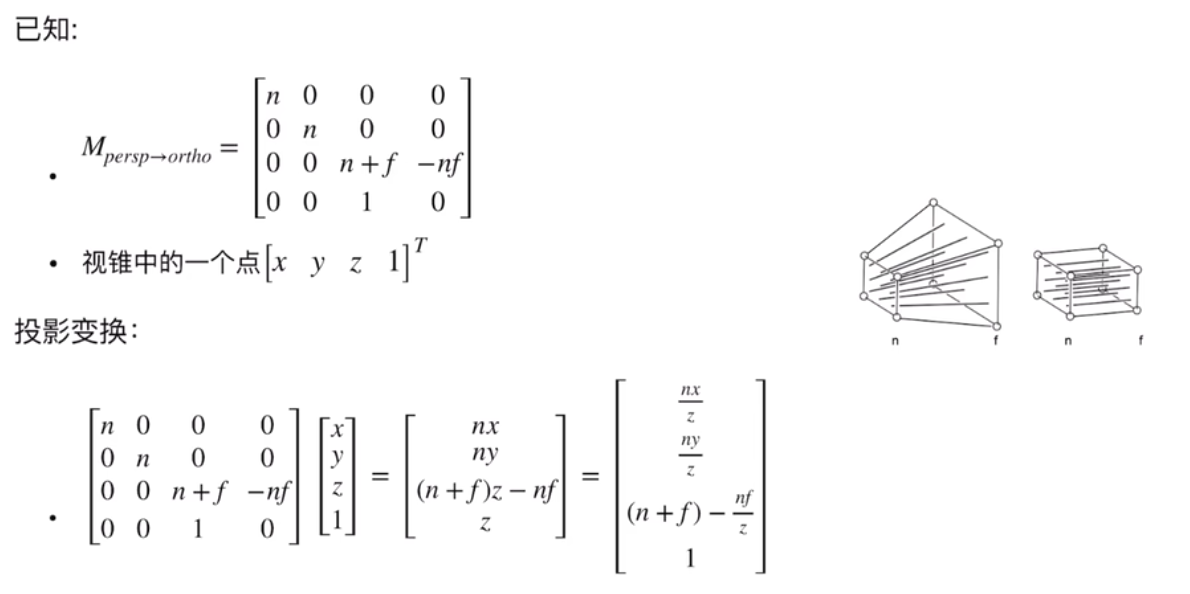
透视投影 → 正交投影
球谐函数
定义了3D高斯椭球的颜色
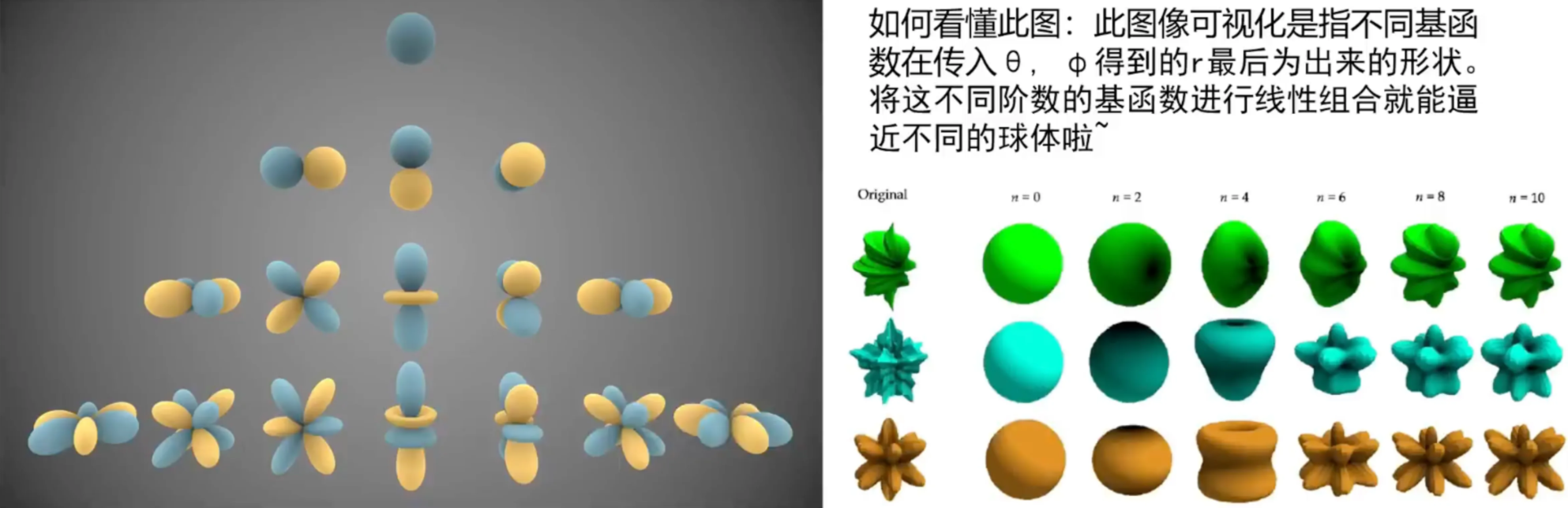

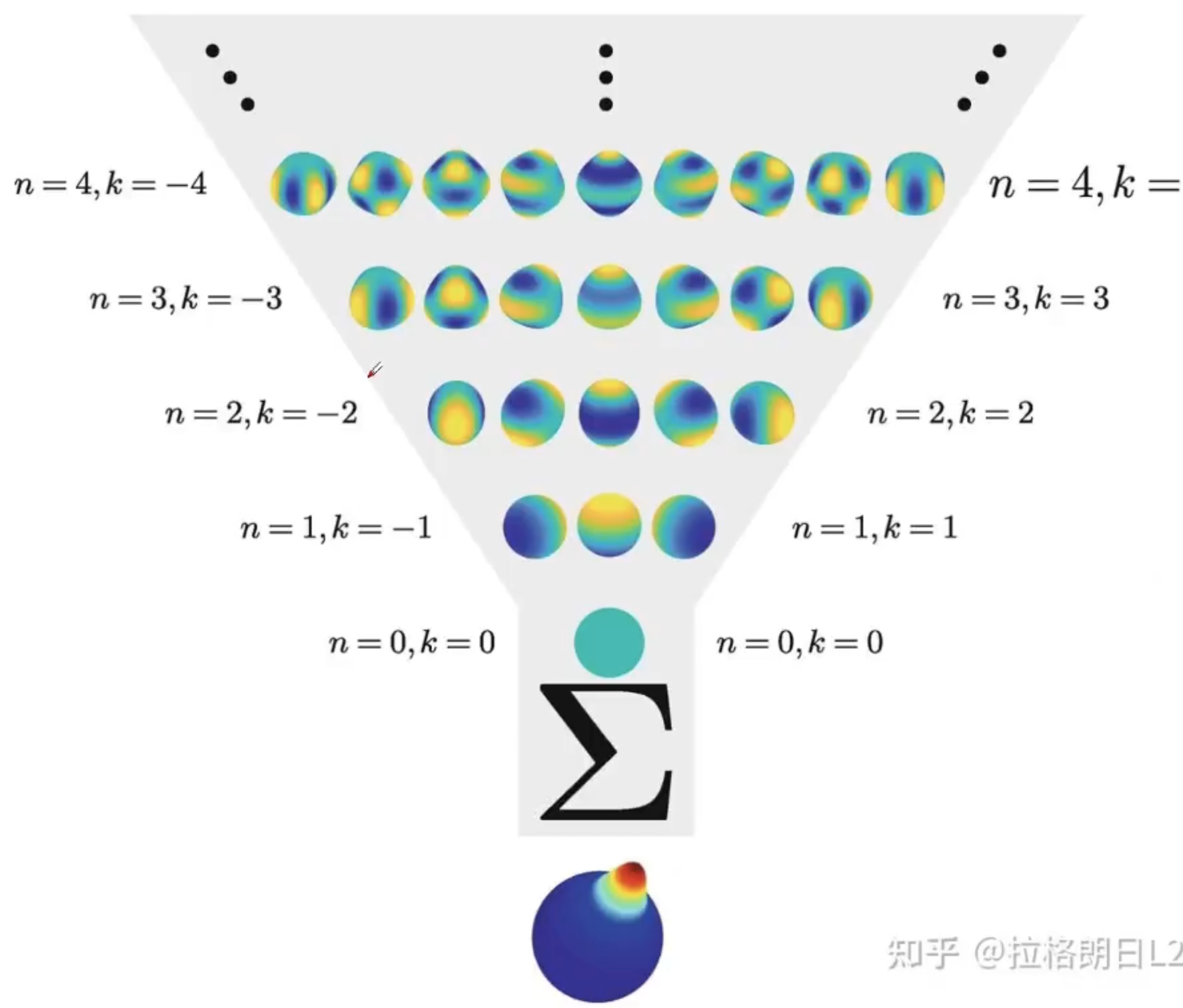
类似于傅立叶级数,由一组能代表球面上不同位置(不同颜色值)的值基函数, 阶数越高表达能力越强
球谐函数只和 $\theta$ (z 轴夹角), $\phi$ (点在x-y平面上的投影与x-轴正方向的夹角) 有关: $r = f(\theta,\phi)$
球谐函数如下:
\[f(t) \approx \sum_{l} \sum_{m=-l}^{l} c_l^m Y_l^m(\theta, \phi) = c_0^0 Y_0^0 + \left(c_1^{-1} Y_1^{-1} + c_1^0 Y_1^0 + c_1^1 Y_1^1\right) + \left(c_2^{-2} Y_2^{-2} + c_2^{-1} Y_2^{-1} + c_2^0 Y_2^0 + c_2^1 Y_2^1 + c_2^2 Y_2^2\right) + c_3^{-3} Y_3^{-3} + \dots\]- l: 控制阶数
- c: 可训练参数
参数量是阶数的平方
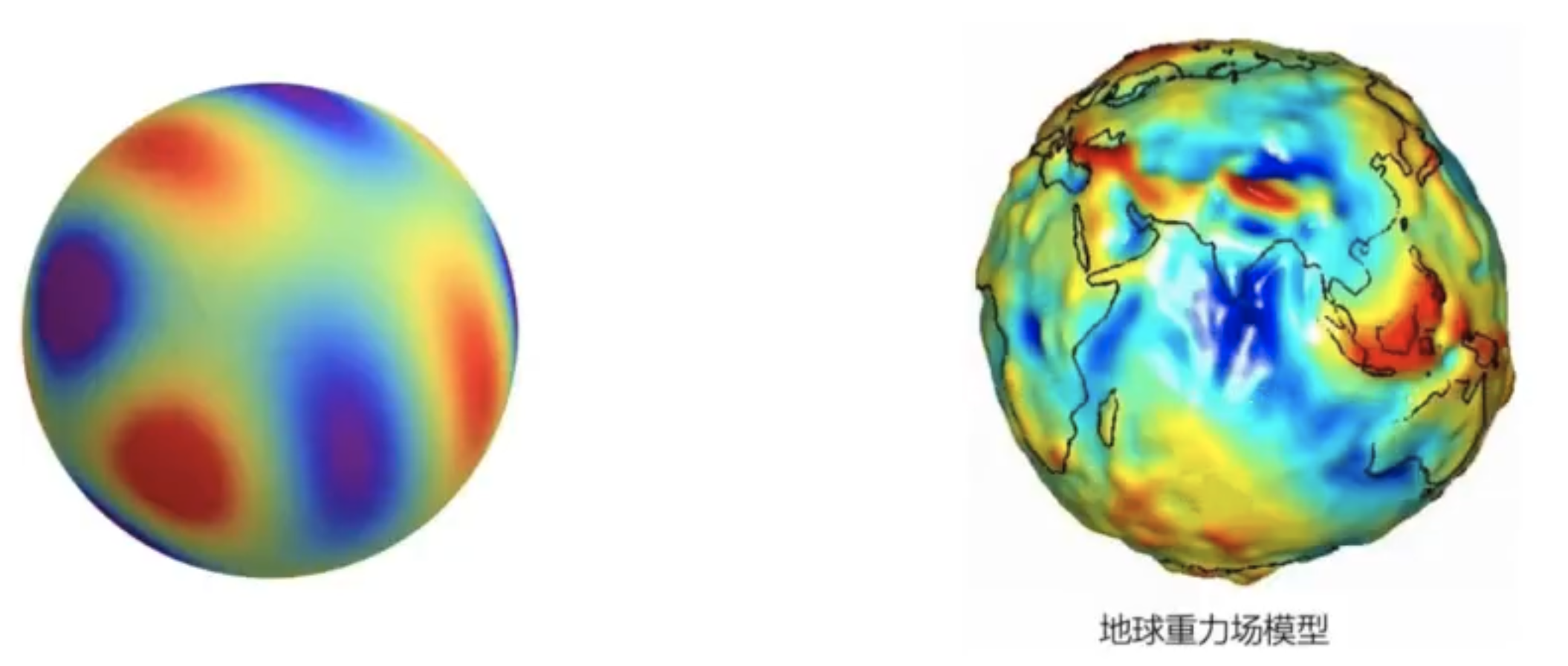
球谐函数用于表达不同角度的颜色表达
通过球谐函数来表达, 使3D高斯椭球在不同角度呈现不同颜色
原文中采用4阶:
参数量为 \(3*(4^2) = 3*16 = 3+45 = 48\)
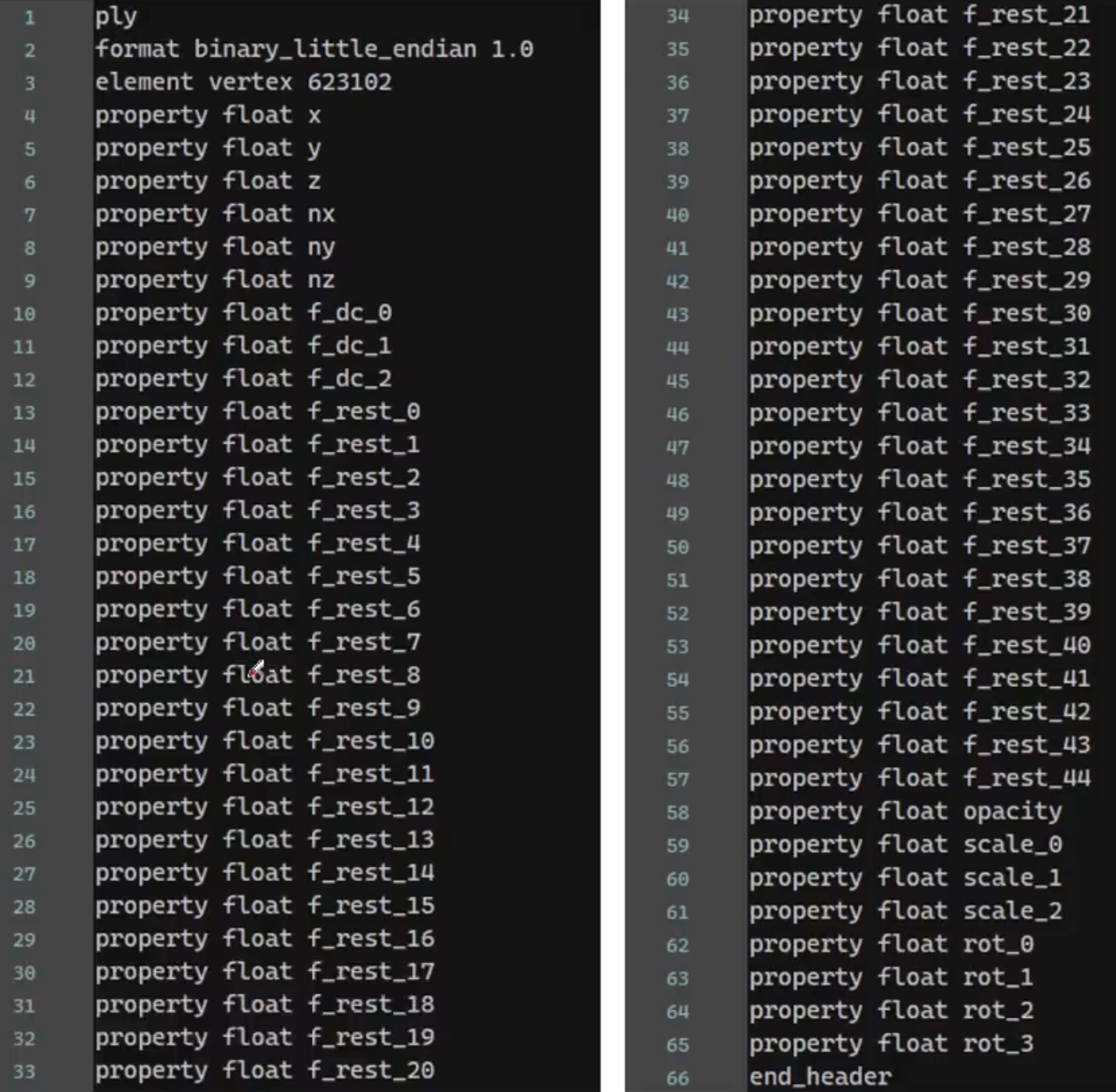
迭代参数
每个3D高斯椭球的参数包括:
- 中心点位置: (x, y, z)
- 协方差矩阵: R, S
- 球谐函数系数: 16 x 3
- 透明度: $\alpha$
渲染(砸雪球)
g.footprint 是一个 3D Gaussian 投影到屏幕平面后的覆盖范围大小。
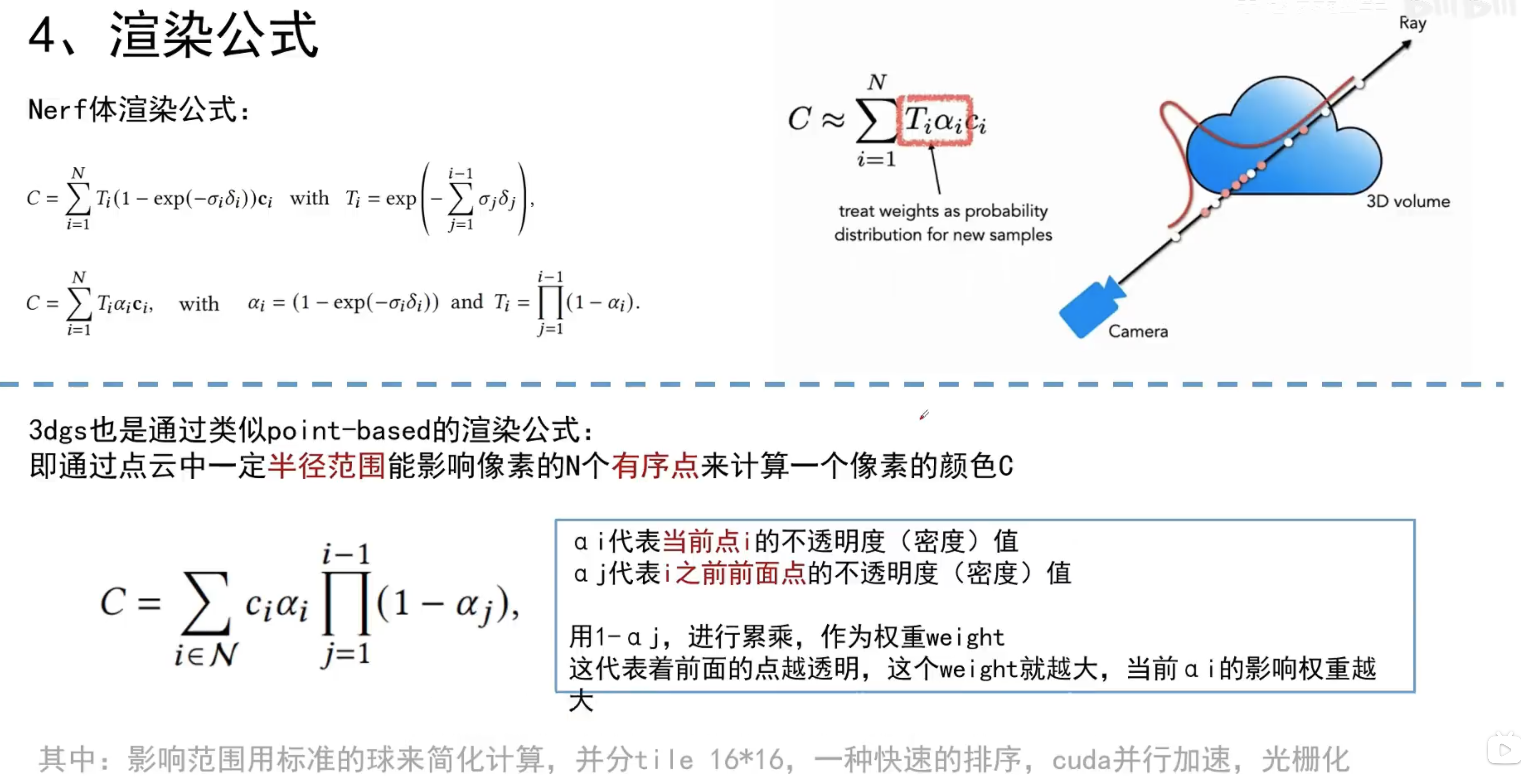
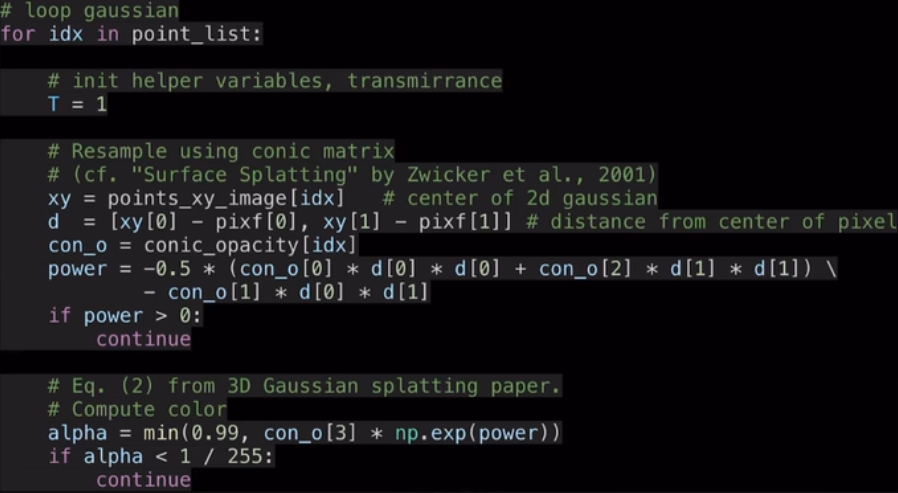
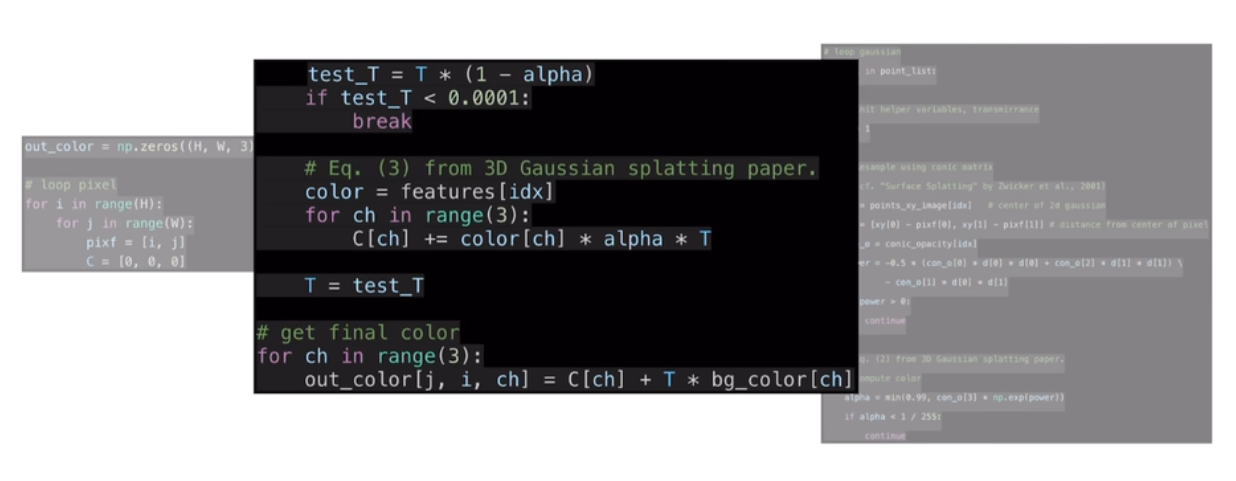
注意:
- T(s): 在s点之前,光线没有被阻碍的概率
- alpha = 原本高斯椭球的透明度 * power of gaussian(远离中心点造成的强度影响)
渲染方式比Nerf的快:
- Splatting 没有找粒子的过程
- 需要对高斯球按照深度z排序
Output
# Rasterize visible Gaussians to image, obtain their radii (on screen).
rendered_image, radii, depth_image = rasterizer(
means3D=means3D,
means2D=means2D,
shs=shs,
colors_precomp=None,
opacities=opacity,
scales=scales,
rotations=rotations,
cov3D_precomp=None)
rendered_image = viewpoint_camera.postprocess(viewpoint_camera, rendered_image)
Adaptive Density Control
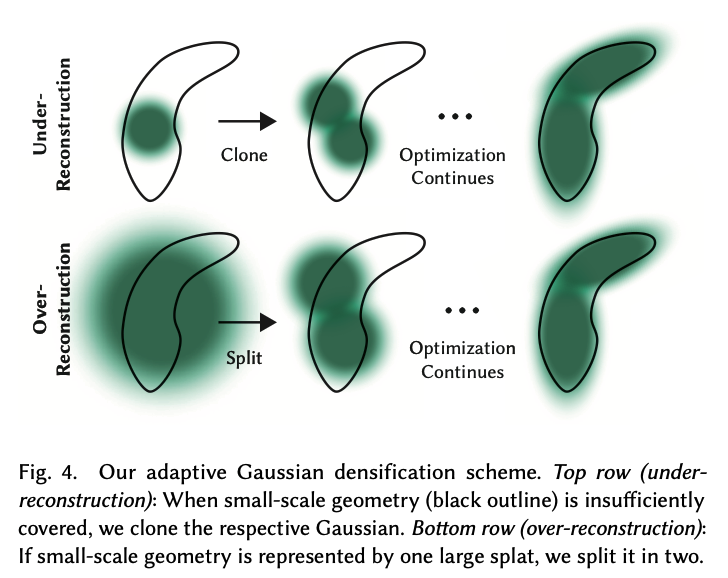
比如每隔100个epoch会判断点云分布是否合理
- Pruning (减少伪影的出现): 透明度低于阈值 或者离相机近的点会被删除
- Densification (过度重构或者欠采样)(基于梯度变化来判断):
- Under-reconstruction: 方差小 → 克隆高斯来适应
- Over-Reconstruction: 方差很大 → 分裂成两个高斯

Enjoy Reading This Article?
Here are some more articles you might like to read next: