3D Gaussian Ray Tracing: Fast Tracing of Particle Scenes

https://arxiv.org/abs/2407.07090

https://gaussiantracer.github.io/

Overview

• A fast differentiable ray tracer for semi-transparent particle-based scene representations such as Gaussians.
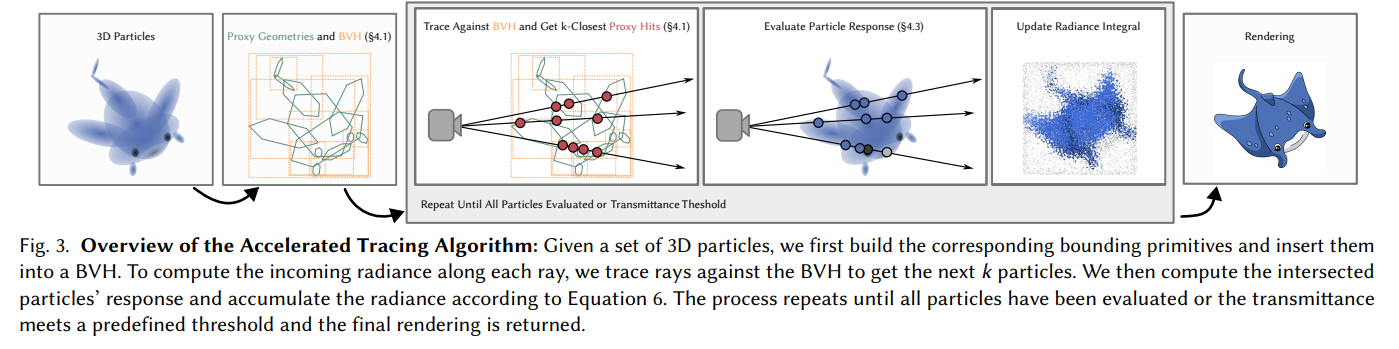
• The main idea is to construct encapsulating primitives around each particle, and insert them into a BVH to be rendered by a ray tracer specially adapted to the high density of overlapping particles.
• 和Relightable 3DGS对比：
  • Relightable 3DGS use axis-aligned bounding boxes (AABBs) to enclose particles, which results in approximately 3× lower FPS during inference compared to the stretched icosahedrons employed in our optimized tracer。
  • Relightable 3DGS Ray tracing（光线追踪）只在训练阶段用，3D Gaussian Ray Tracing采用优化过的 ray-tracing，并且在训练和推理阶段都统一用它来渲染, which allows for inserting objects, refraction, lens distortion, and other complex effects.

Background

Ray

\[\mathbf{r}(\tau) = \mathbf{o} + \tau \mathbf{d}\]

• \(\mathbf{o} \in \mathbb{R}^3\) 是光线起点 (ray origin)
• \(\mathbf{d} \in \mathbb{R}^3\) 是光线方向 (ray direction，通常单位化)
• \(\tau \in [\tau_n, \tau_f]\) 光线沿着方向 d 穿过场景，从近裁剪面到远裁剪面。

Hardware-Accelerated Ray Tracing

• RTX Core
  • 专门用于加速光线追踪计算，不自己调度线程，不管理共享内存，它只是一个硬件加速器。
  • 硬件级别处理光线与场景几何体的相交计算（ray-triangle 或 ray-AABB intersection）。
  • 加速 BVH traversal（Bounding Volume Hierarchy 遍历）
    • BVH traversal 的核心思想是：光线沿路径只与与其相交的包围体递归求交，从而跳过大部分不相交的区域，只对真正可能命中的粒子做精确计算。
• SM（Streaming Multiprocessor）
  • 执行 CUDA 核心（threads），处理着色、物理模拟、AI 推理、通用 GPU 计算
  • 管理寄存器、共享内存和调度线程块。
  • 内部有 FP32、FP64 运算单元、整数单元、Tensor cores（用于 AI 推理加速）。
• NVIDIA OptiX
  • ray-gen program： where the SMs may initiate a scene traversal for a given ray.
  • intersection program：对硬件不直接支持的粒子做精确求交
  • any-hit program : during the traversal for every hit and may further process or reject the hit.
  • closest-hit program: at the end of the traversal, for further processing of the closest accepted hit.
  • miss program：at the end of the traversal for further processing when no hit has been accepted.
  • 这种管线对于不透明物体非常高效，因为命中次数少。但半透明粒子/体积渲染要求光线可能穿过大量粒子，每条光线需要处理多次命中，传统光追效率下降。

Method

Adaptive bounding mesh primitives

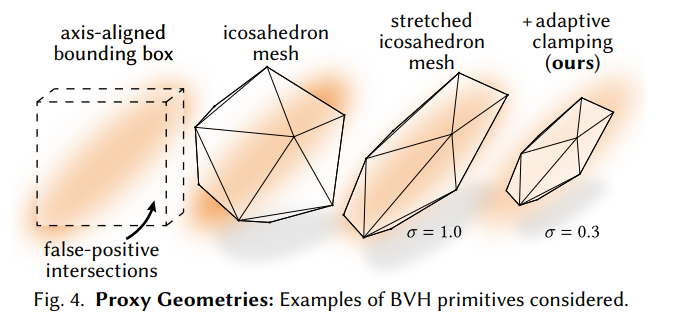
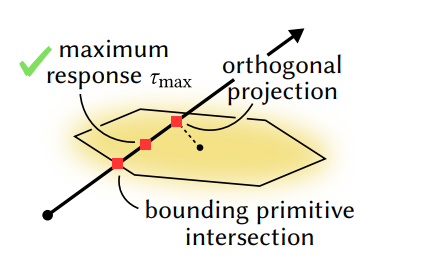
Gaussian particles will cause the traversal to have to evaluate many false-positive intersections which actually contribute almost nothing to the rendering.

Stretched Polyhedron Proxy Geometry: regular icosahedron mesh (正12面体)

• Precisely, for each particle we construct an icosahedron with a unit inner-sphere
  • Scale Transform: \(\mathbf{v} \leftarrow \sqrt{2 \log \!\left(\frac{\sigma}{\alpha_{\min}}\right)} \, \mathrm{SR^T} \, \mathbf{v} + \boldsymbol{\mu}\) 重新定义每个vertex的位置
  • \(\alpha_{\min}\) (typically = 0.01)
    • 12面体可以比椭球小 但是\(\alpha_{\min}\)以上的部分 must be captured

• Evaluating Particle Response (渲染)(我理解就是选颜色)：

  How to compute the contribution of each particle to the ray

  • 射线与粒子相交后，需要决定：沿射线的哪个位置（参数 \(\tau\)）来取样粒子的贡献
  • \[\tau_{\max} = \arg\max_{\tau} \, \rho(\mathbf{o} + \tau \mathbf{d}) = \frac{(\boldsymbol{\mu} - \mathbf{o})^{T} \Sigma^{-1} \mathbf{d}} {\mathbf{d}^{T} \Sigma^{-1} \mathbf{d}} = \frac{-\mathbf{o}_{g}^{T} \mathbf{d}_{g}} {\mathbf{d}_{g}^{T} \mathbf{d}_{g}}\]
    • \[\mathbf{o}_{g} = S^{-1} R^{T} (\mathbf{o} - \boldsymbol{\mu}), \quad \mathbf{d}_{g} = S^{-1} R^{T} \mathbf{d}.\]

Ray Tracing Renderer

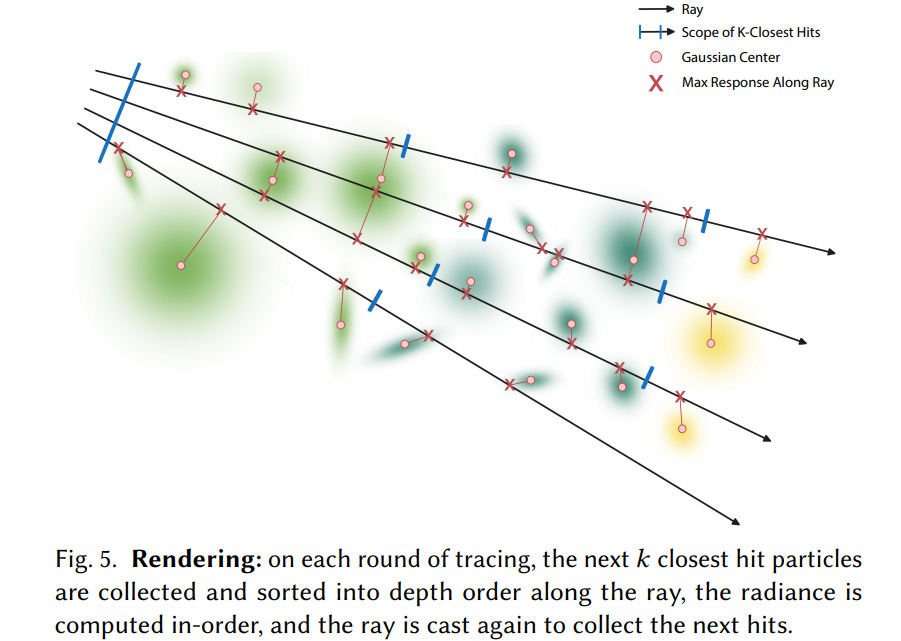
Tracing semi-transparent surfaces or particles

• BVH 加速结构
  • 使用 ray-gen program（生成射线的着色器程序）在 BVH（bounding volume hierarchy，加速结构）中追踪射线。
  • 找到射线接下来会遇到的 k 个粒子（粒子用包围体表示）。
  • 在这一阶段：
    • 使用 any-hit program，它不会立即计算粒子响应，而是仅仅 收集相交的粒子索引，并保持它们的顺序。
    • 好处：避免重复计算，提高效率。
• 遍历已排序的粒子列表
  • ray-gen program 拿到一组已排序的相交粒子（primitive hits）
  • 按顺序取出每个粒子，并渲染它们的贡献
• 迭代过程
  • 处理完这批 k 粒子后，从最后一个渲染的粒子位置继续，再发射一条新的射线，继续寻找接下来的 k 粒子
  • 不断重复，直到所有相交粒子都处理完。
• 提前终止（Early Termination）
  • 如果在处理过程中，累积的粒子密度让射线的透射率 低于某个阈值 \(T_{\min}\)
  • 那么可以提前终止（因为几乎没有光能量能穿透，后续粒子贡献可以忽略）

Optimization

• 采用 3DGS的优化策略
• 不同点：3DGS方法依赖于屏幕空间梯度，这里采用世界坐标系中的梯度，因为更通用。
• Training with Incoherent Rays

Particle Kernel Functions

Our formulation does not require the particles to have a Gaussian kernel, enabling the exploration of other particle variants.

• 标准 3D Gaussian
  • \[\hat{\rho}(\mathbf{x}) = \sigma \exp\Big[-(\mathbf{x}-\boldsymbol{\mu})^T \Sigma^{-1} (\mathbf{x}-\boldsymbol{\mu}) \Big]\]
• 广义 Gaussian (Generalized Gaussian) of degree n
  • \[\hat{\rho}_n(\mathbf{x}) = \sigma \exp\Big[- \big((\mathbf{x}-\boldsymbol{\mu})^T \Sigma^{-1} (\mathbf{x}-\boldsymbol{\mu}) \big)^n \Big], \quad n=2\]
• Kernelized Surface: 2DGS
• Cosine Wave Modulation（余弦调制）
  • \[\hat{\rho}_c(\mathbf{x}) = \hat{\rho}(\mathbf{x}) \Big( 0.5 + 0.5 \cos \big( \psi \, (S^{-1} R^T (\mathbf{x}-\boldsymbol{\mu}))_i \big) \Big)\]
  • 𝜓 an optimizable parameter.

Relightable 3D Gaussian: Real-time Point Cloud Relighting with BRDF Decomposition and Ray Tracing

https://nju-3dv.github.io/projects/Relightable3DGaussian/

https://arxiv.org/abs/2311.16043

目标

Introduce a novel pipeline tailored for decomposing material and lighting from a collection of multiview images based on 3DGS, supporting relighting, editing, and ray tracing of a reconstructed 3D point cloud.

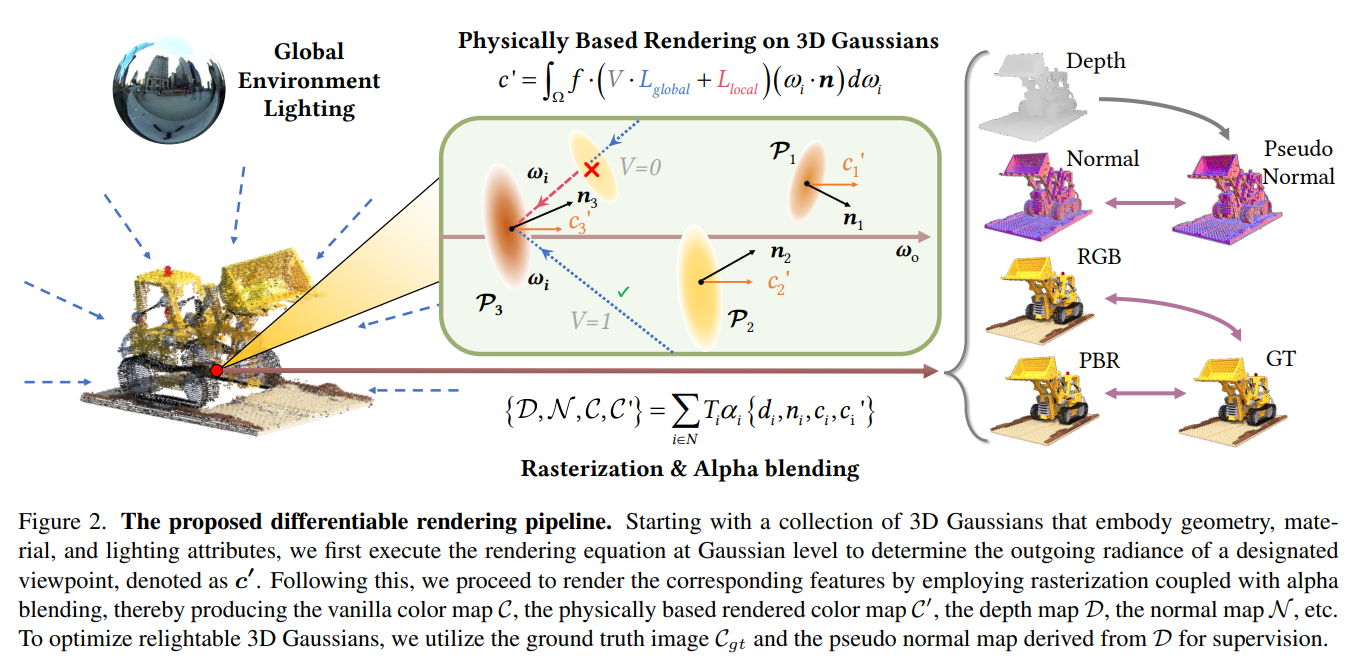
推理阶段不走 ray tracing，而是 点渲染 (Gaussian Splatting) 加 着色 (shading)

换光照：只要在推理阶段换掉 \(L_i\)（光源的位置、方向、颜色），渲染就会反映新的光照条件, 只考虑了直接光照（光源到点的一次反射).

Geometry Enhancement

Normal Estimation

• Incorporate a normal attribute n for each 3D Gaussian
• An optimization of n from initial random vectors via back-propagation
• \(\{D, N\} = \sum_{i \in \mathcal{N}} T_i \alpha_i \{d_i, n_i\}\) rendering the depth and normal map for a specified viewpoint. $d_i$ and $n_i$ denote the depth and normal of the point.
• \(L_n = \lVert N - \tilde{N} \rVert_2\) : N: 渲染网络学出来的法向量; $\tilde{N}$: 由MVS深度 $D_{\text{mvs}}$ 导出的几何一致性约束

Multi-View Stereo as Geometry Clues

• \[L_d = \lVert D - D_{mvs} \rVert_1\]
  • Ensure consistency between the rendered depth D and the filtered MVS depth map \(D_{mvs}\)
  • utilize Vis-MVSNet to estimate per-view depth map \(D_{mvs}\)

BRDF and Light Modeling

渲染方程回顾（Rendering Equation）

\[L_o(\omega_o, x) = \int_{\Omega} f(\omega_o, \omega_i, x) \, L_i(\omega_i, x) \, (\omega_i \cdot n) \, d\omega_i\]

• x：表面点
• n：表面法向量
• \(\omega_i\)：入射光方向
• \(\omega_o\)：出射光方向（观察方向）
• \(L_i(\omega_i, x)\)：入射光亮度
• \(f(\omega_o, \omega_i, x)\)：BRDF，描述材质反射特性
• \(\Omega\)：半球域（表面上方的所有方向）

PBR on 3DGS & Parameter Set

在3D Gaussian 层级上计算 PBR color，再通过 alpha-blending 渲染图像。

\[C' = \sum_{i \in N} T_i \alpha_i c'_i\]

• \(c'_i\) 是对原 \(c_i\) 的“物理化增强”, 更符合真实世界光照和材质的物理规律

Assign additional BRDF properties to each Gaussian: a base color b ∈ [0, 1], a roughness r ∈ [0, 1] and a metallic m ∈ [0, 1]

PBR 颜色算法

\[c'(\omega_a) = \sum_{i=0}^{N_s} \big(f_d + f_s(\omega_o, \omega_i)\big) \, L_i(\omega_i) \, (\omega_i \cdot n) \, \Delta \omega_i\]

• 采用简化 Disney BRDF 模型，分解BRDF：\(f(\omega_o, \omega_i)=f_d + f_s\)
  • 漫反射：\(f_d = \frac{1 - m}{\pi} \cdot b\)
  • 镜面反射项：\(f_s(\omega_o, \omega_i) = \frac{D(h; r) \cdot F(\omega_o, h; b, m) \cdot G(\omega_i, \omega_o, h; r)} {(n \cdot \omega_i) (n \cdot \omega_o)}\)
  • where h is the half vector, D, F and G represent the normal distribution function, Fresnel term and geometry term.
• 入射光建模 (Incident Light Modeling), 将入射光分解为 全局 + 局部 两部分：
  • \[L_i(\omega_i) = V(\omega_i) \cdot L_{\text{global}}(\omega_i) + L_{\text{local}}(\omega_i)\]
    • the visibility term V and the local light term \(L_{local}\) are parameterized as Spherical Harmonics (SH) for each Gaussian, denoted as v and l respectively
    • The global light term is parameterized as a globally shared SH, denoted as \(l^{env}\)
    • V 只需用 少量随机光线的透射T 来做监督训练
• For each 3D Gaussian, we sample \(N_s\) incident directions over the hemisphere space through Fibonacci sampling to provide numerical integration.

The i-th Gaussian \(P_i\) is parameterized as \(\{µ_i, q_i, s_i, o_i, c_i, n_i, b_i, r_i, m_i, v_i,l_i\}\)

• \(c_i\) 之后都是这篇文章加的

Regularization

实施正则化是为了促进材质和光照的合理分解。

Base Color Regularization

\[C_b = \sum_{i \in N} T_i \alpha_i b_i\] \[L_b = \lVert C_b - C_{target} \rVert_1\]

• Ideal base color should exhibit certain tonal similarities with the observed image C while remaining free from shadows and highlights.
• We generate an image \(C_{target}\) with reduced shadows and highlights, serving as a reference for the rendered base color \(C_b\)
• \[C_{target}=w⋅C_h+(1−w)⋅C_s\]
  • \(C_s = 1 − (1 − C)²\) → 阴影减弱图（shadow-reduction）
  • \(C_h = C²\) → 高光减弱图（highlight-reduction）
  • \(w = 1 / (1 + e^{-ψ(C_v - 0.5)})\) → 权重，决定阴影和高光哪个占更多
    • ψ experimentally set to 5
    • \(C_v = max(R, G, B)\) is the value component of HSV color

Light Regularization

\[L_{\text{light}} = \sum_{c \in \{R, G, B\}} \left( L_c - \frac{1}{3} \sum_{c \in \{R, G, B\}} L_c \right)\]

• 假设入射光接近自然白光
• 通过正则约束光的三通道不要差别太大 → 避免偏色
• 让光尽量接近白色（R、G、B 三个通道均衡），防止渲染出来颜色偏红偏蓝。

双边平滑约束 (Bilateral Smoothness)

只是拿m举例，其他的 r,b 都是一样的道理

\[L_{s,m} = \|\nabla M\| \, \exp\big(- \|\nabla C_{\text{gt}}\|\big)\]

• M = 渲染出的金属度图 \(M = \sum_i T_i \alpha_i m_i\)
• 对 金属度、粗糙度、基础色 都加类似约束
• 如果图像颜色平滑 → 材质属性也应该平滑
• 颜色变化大的地方 → 不约束材质属性
• 防止出现材质参数在颜色平滑区域跳变 → 保持自然

Point-based Ray Tracing

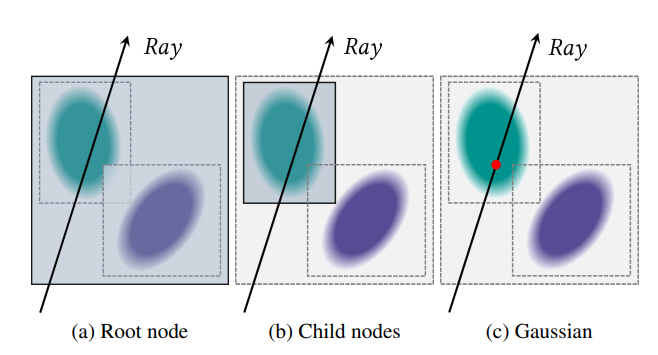
BVH（Bounding Volume Hierarchy）

核心思想：通过包围体快速判断光线是否可能与节点内物体相交，从而避免遍历所有物体。

是一种用于加速光线追踪的 空间索引数据结构：

• 树形结构，把场景中的物体（或 3D Gaussian）按 层级包围盒 组织起来
• 每个节点存储一个 Bounding Volume（包围体）（文本中用的是bounding box——axis-aligned bounding boxes (AABBs)）
  • 内部节点：包住它所有子节点的包围体
  • 叶节点：包住单个物体（或 Gaussian）的 bounding box
• 用 二叉基数树（binary radix tree），可以并行构建，支持训练过程中的实时 BVH 更新。
  • 一棵 Binary Radix Tree 是整个 3D 空间的索引结构
  • 树里的 每个叶节点 对应一个 单独的 bounding box of a Gaussian
  • 树里的 内部节点 是它的两个孩子的 包围盒的组合
  • 光线穿过场景 → 从根节点开始递归 →光线穿透半透明 Gaussian → 遇到叶节点累积 αj → 继续递归回到上层节点，遍历其他相交的叶节点
• 更新透射，当透射值T低于阈值 \(T_{\min}\) 时，提前终止光线追踪 → 提高速度
  • \[T_i = (1 - \alpha_{i-1}) T_{i-1}, \quad \text{for } i = 1, \dots, j-1, \quad \text{with } T_1 = 1\]

Visibility Estimation and Baking

\[L_v = \lVert V - T \rVert_2\]

• V 是模型可学习的 visibility
• T 是通过光线追踪计算的 baked visibility

Realistic Relighting 流程

• 第一步：可见性微调（Finetune visibility）
  • 每个 Gaussian 的可见性 v（烘焙的 V）会通过光线追踪微调
  • 更新 对象之间的遮挡关系（occlusion correlations）
• 第二步：Gaussian 级 PBR
  • 对每个 Gaussian 计算PBR 颜色 \(c'_i\)
• Step 3：Alpha Blending

Training

• 30,000 iterations in the initial stage
  • optimize an 3DGS model, augmented with an additional normal vector n
  • also add normal gradient condition for adaptive density control
• 10,000 iterations in stage 2
  • begin with the ray tracing method to bake the visibility term v
  • optimize the entire parameter set
  • \(N_s = 24\) rays per Gaussian for PBR

Stage 1:

• \[L_n = \lVert N - \tilde{N} \rVert_2\]
• \[L_d = \lVert D - D_{mvs} \rVert_1\]

Stage 2:

• \[L_b = \lVert C_b - C_{target} \rVert_1\]
• \[L_{\text{light}} = \sum_{c \in \{R, G, B\}} \left( L_c - \frac{1}{3} \sum_{c \in \{R, G, B\}} L_c \right)\]
• \[L_{s,m} = \|\nabla M\| \, \exp\big(- \|\nabla C_{\text{gt}}\|\big)\]
  • 只是拿m举例，其他的 r,b 都是一样的道理
• \[L_v = \lVert V - T \rVert_2\]