DENOISING DIFFUSION IMPLICIT MODELS

DDIM is a generalization of DDPM. DDPM is a special case of DDIM when $\sigma_t^2 = \tilde{\sigma}t^2 = \frac{1 - \bar{\alpha}{t-1}}{1 - \bar{\alpha}_t} \beta_t.$

和DDPM比 就改了一个 mean 和一个 std 的算法， 模型输入输出并不发生变化

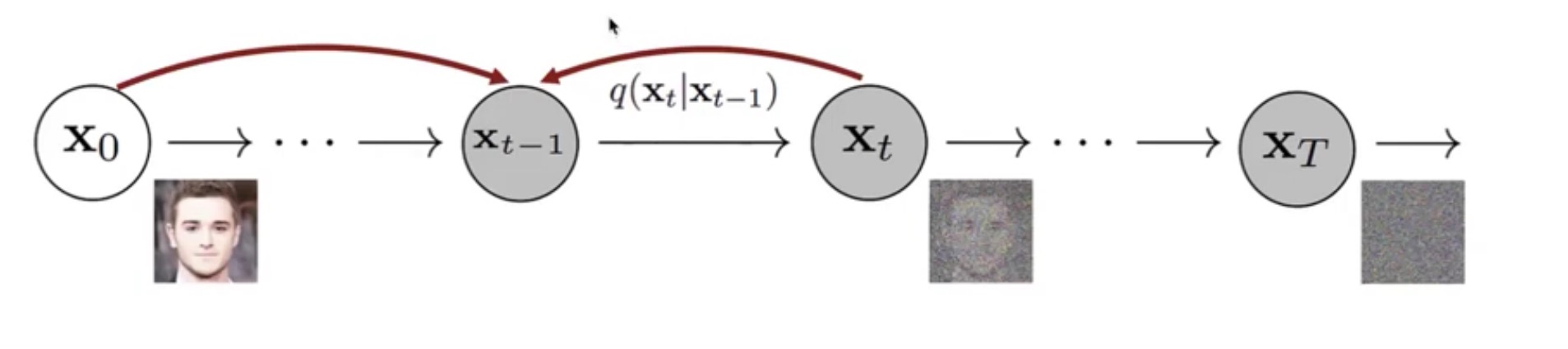
Forward Process

In the forward process $q_\sigma(x_{1:T} \mid x_0) := q_\sigma(x_T \mid x_0) \prod_{t=2}^{T} q_\sigma(x_{t-1} \mid x_t, x_0)$ :

• $x_T$ is sampled from $x_0$ first.
• Each $x_{t-1}$is sampled from $x_t$ and $x_0$ in a reverse manner.

Reverse Process

Define $q_\sigma(x_{t-1} \mid x_t, x_0)$ and make sure $q_\sigma(x_{t} \mid x_0) = \mathcal{N}\left( \sqrt{\alpha_T} \mathbf{x}_0, (1 - \alpha_T) \mathbf{I} \right)$ remains the same as in DDPM.

\[q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}\left( \sqrt{\alpha_{t-1}} \mathbf{x}_0 + \sqrt{1 - \alpha_{t-1} - \sigma_t^2} \cdot \frac{\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_0}{\sqrt{1 - \alpha_t}}, \sigma_t^2 \mathbf{I} \right)\]

The noise predictor trained for DDPM can be directly used in the DDIM reverse process. You can perform the DDPM or DDIM reverse process using the same noise predictor.

Parameterize $\sigma_t$

\[\sigma_t = \eta \sqrt{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t}} \beta_t\]

• $\eta = 0$ : Deterministic process. For the same $\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$, we always obtain the same $x_0$
• $\eta = 1$: Same as DDPM

Accelerating Sampling Process

Consider a sub-sequence (S) of the time steps: $\tau = [\tau_1, \tau_2, \dots, \tau_S].$

The reverse process for this sub-sequence: $p_\theta(\mathbf{x}\tau) = p(\mathbf{x}_T) \prod{t=1}^S p_\theta(\mathbf{x}{\tau{i-1}} \mid \mathbf{x}_{\tau_i})$ 

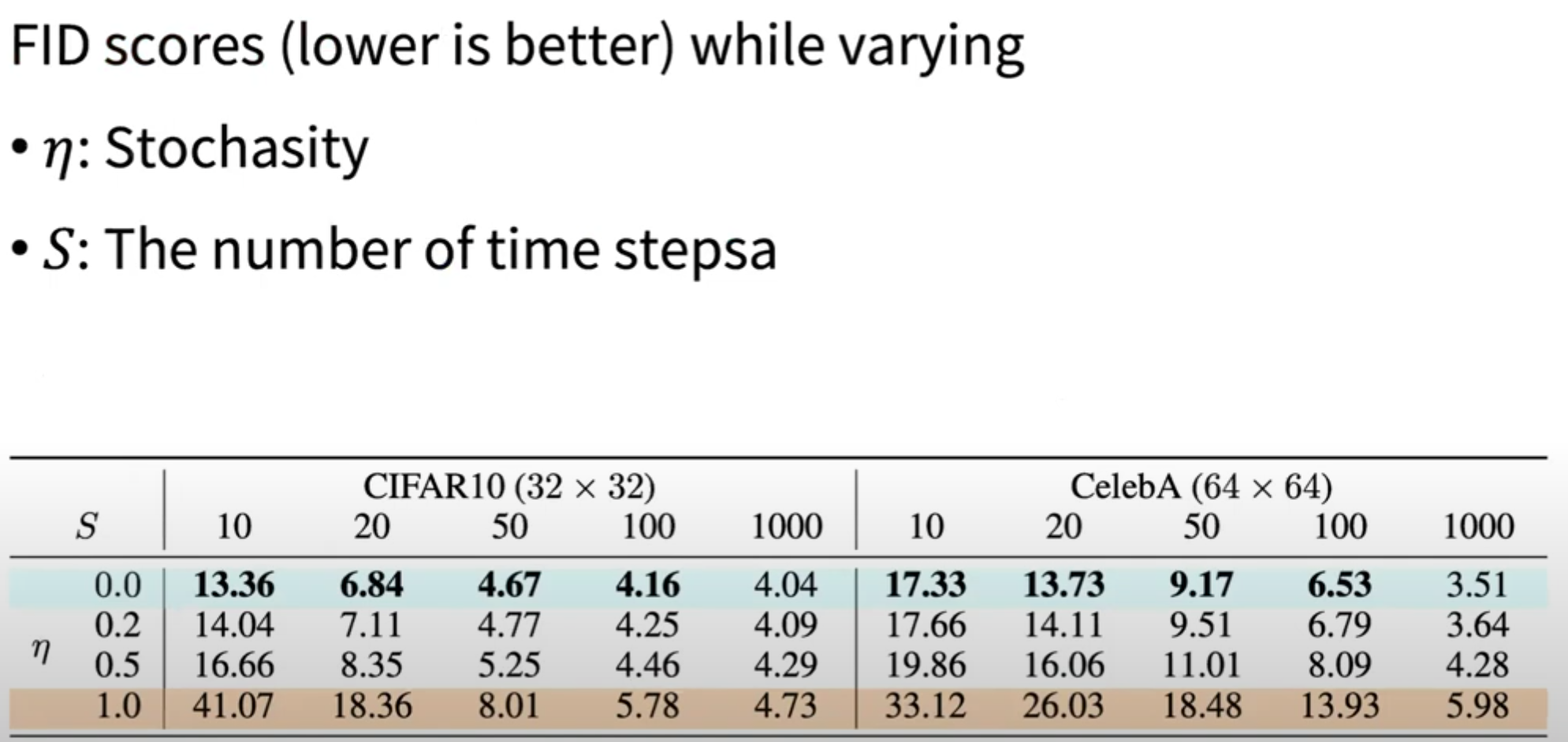
As smaller time steps are used, the quality of the generated data can worsen.

Quality degradation is mitigated when the DDIM reverse process becomes more deterministic.