DDPM

网络输出是对应时刻的噪声 $z_t$ 输入是图像 $x_t$, 它们的shape大小一致
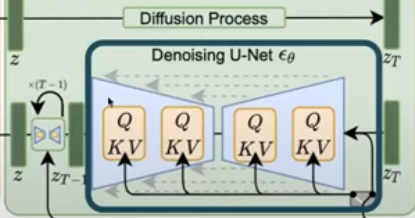
Earlier models used U-Net with the attention module at each layer for the noise prediction.
- Self-attention
- Q & K & V: The outputs of each U-net layer.
- Cross-attention
- Q: The output of each U-net layer
- K & V: The outputs from the input condition encoder.
扩散过程(Forward Process)
$a_t = 1 - \beta_t$ , $\beta_t$要越来越大,论文中0.0001到0.002,从而a也就是要越来越小
$x_t = \sqrt{a_t}x_{t-1} + \sqrt{1- a_t} z$
z是满足高斯分布的噪音

$x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1-\bar{\alpha}_t} z$
\[q({x}_t \mid {x}_0) = \mathcal{N}({x}_t; \sqrt{\bar{\alpha}_t} {x}_0, (1 - \bar{\alpha}_t)\mathbf{I})\]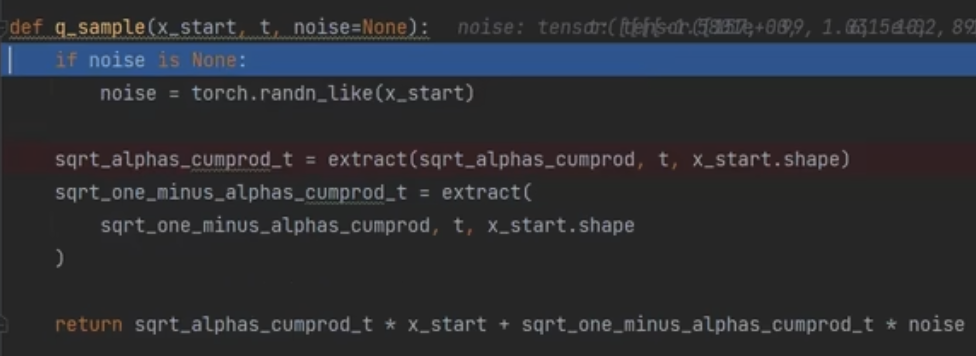
去噪过程(Reverse Process)
\[p({x}_{t-1} \mid {x}_t, {x}_0) = p({x}_t \mid {x}_{t-1}, {x}_0) \frac{p({x}_{t-1} \mid {x}_0)}{p({x}_t \mid {x}_0)}\] \[\propto \exp\left( -\frac{1}{2}\frac{\left(x_t - \sqrt{\alpha_t} x_{t-1}\right)^2}{\beta_t} - \frac{\left(x_{t-1} - \sqrt{\bar{\alpha}_t} x_0\right)^2}{1 - \bar{\alpha}_t} \right)\] \[= \exp\left( -\frac{1}{2} \left[ \left(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}\right)x_{t-1}^2 - \left(\frac{2\sqrt{\alpha_t}}{\beta_t}x_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} x_0\right)x_{t-1} + C(x_t, x_0) \right] \right)\]其中 $C(x_t, x_0)$是常数项,不影响优化.
因为 $\exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) = \exp\left( -\frac{1}{2}\left( \frac{1}{\sigma^2}x^2 - \frac{2\mu}{\sigma^2}x + \frac{\mu^2}{\sigma^2} \right) \right)$, 能得到均值和方差: (方差固定不不变)
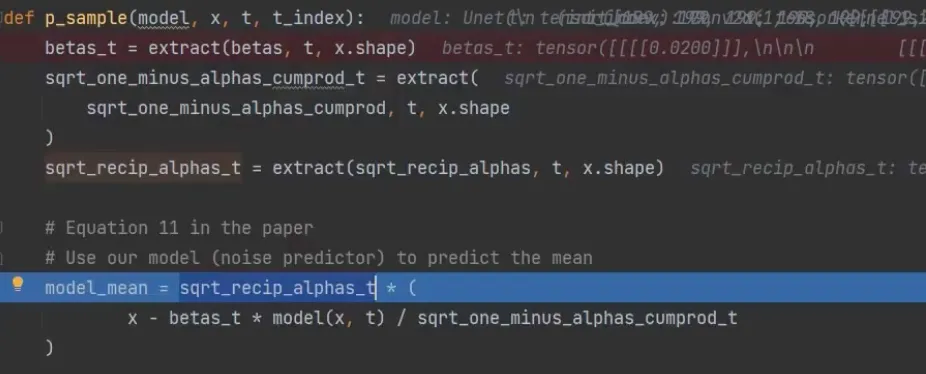
\[\tilde{\mu}_t({x}_t, {x}_0) = \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} x_t + \frac{\sqrt{\bar{\alpha}_t} \beta_t}{1 - \bar{\alpha}_t} x_0\]之前 xt 可以通过$x_t$$x_0$ 得到,逆运算可得 $\mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}} \left( \mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \mathbf{z}_t \right)$ 所以最后得到:
\[\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} (x_t -\frac{ \beta_t}{\sqrt{1 - \bar{\alpha}_t}} z)\]所有都是已知数除了噪声z, 我们需要通过机器学习求出它
Trainning & Sampling

Trainning
x_noisy 的 shape 和 输入网络的 的 $x_t$ 大小一致
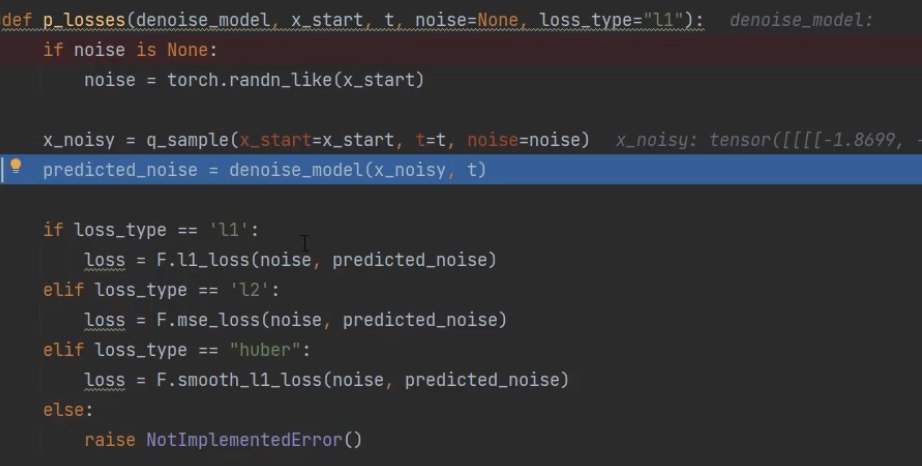
t 在 Unet 中 被用类似 positional embedding 的方式注入 x_noisy
Sampling

Enjoy Reading This Article?
Here are some more articles you might like to read next: