DDIM Deterministic Sampling

if $\sigma_t = 0$ for all t, \(x_{t-1} = \sqrt{\frac{\bar{\alpha}_{t-1}}{\bar{\alpha}_t}} \left( x_t - \sqrt{1 - \bar{\alpha}_t} \, \hat{\epsilon}_\theta(x_t, t) \right) + \sqrt{1 - \bar{\alpha}_{t-1}} \, \hat{\epsilon}_\theta(x_t, t) \\[8pt] = \sqrt{\bar{\alpha}_{t-1}} \left[ \sqrt{\frac{1}{\bar{\alpha}_t}} x_t + \left( \sqrt{\frac{1}{\bar{\alpha}_{t-1}}} - 1 - \sqrt{\frac{1}{\bar{\alpha}_t} - 1} \right) \hat{\epsilon}_\theta(x_t, t) \right]\)

The mapping from $x_T$ to $x_0$ is basically be fixed.

DDIM Inversion

Inverse mapping from $x_0$ to $x_T$ to find the latent space of the $x_0$

Key idea: For the forward process with small time intervals, approximate ( $x_{t+1} - x_t$) by simply replacing $(t -1)$ with $(t+1)$:

\[x_{t-1} - x_t = \sqrt{\bar{\alpha}_{t-1}} \left[ (\sqrt{\frac{1}{\bar{\alpha}_t}} - \sqrt{\frac{1}{\bar{\alpha}_{t-1}}}) x_t + \left( \sqrt{\frac{1}{\bar{\alpha}_{t-1}}} - 1 - \sqrt{\frac{1}{\bar{\alpha}_t} - 1} \right) \hat{\epsilon}_\theta(x_t, t) \right]\] \[x_{t+1} - x_t = \sqrt{\bar{\alpha}_{t+1}} \left[ (\sqrt{\frac{1}{\bar{\alpha}_t}} - \sqrt{\frac{1}{\bar{\alpha}_{t+1}}}) x_t + \left( \sqrt{\frac{1}{\bar{\alpha}_{t+1}}} - 1 - \sqrt{\frac{1}{\bar{\alpha}_t} - 1} \right) \hat{\epsilon}_\theta(x_t, t) \right]\]

Inversion fails when the number of time steps is too small (when the time intervals are too large)

Image Editing using DDIM inversion

1. Perform DDIM inversion using the original prompt in CFG
2. Perform reverse processing using a new prompt in CFG

However, inversion tends to fail when CFG weight w is high:

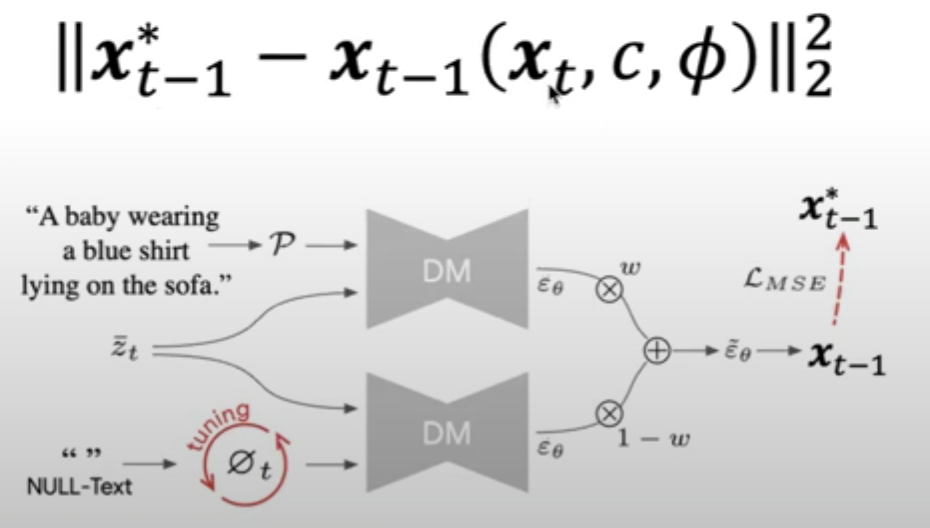
Null-Text Inversion

This method can solve the issue above: Only Null-text $\emptyset$ be tuned