Jacobian matrix

Keywords:

• 泰勒展开
• 线性逼近

目的:

• 可以把非线性变换模拟成一个线性变化

坐标变换:

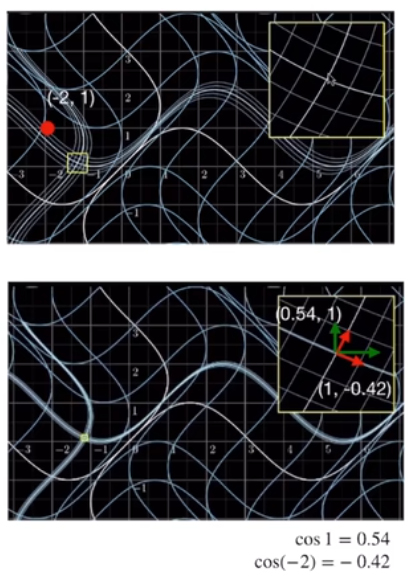
• $f_1(x) = x + \sin(y)$
• $f_2(y) = y + \sin(x)$

Jacobian matrix:

\[\mathbf{J_f} = \begin{bmatrix} \frac{\partial f}{\partial x_1} & \cdots & \frac{\partial f}{\partial x_n} \end{bmatrix} = \begin{bmatrix} \nabla^\top f_1 \\ \vdots \\ \nabla^\top f_m \end{bmatrix} = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}\] \[J = \begin{bmatrix} \frac{\partial f_1}{\partial x} & \frac{\partial f_1}{\partial y} \\ \frac{\partial f_2}{\partial x} & \frac{\partial f_2}{\partial y} \end{bmatrix} = \begin{bmatrix} 1 & \cos(y) \\ \cos(x) & 1 \end{bmatrix}\]

理解：对非线形变换的局部线性性近似。