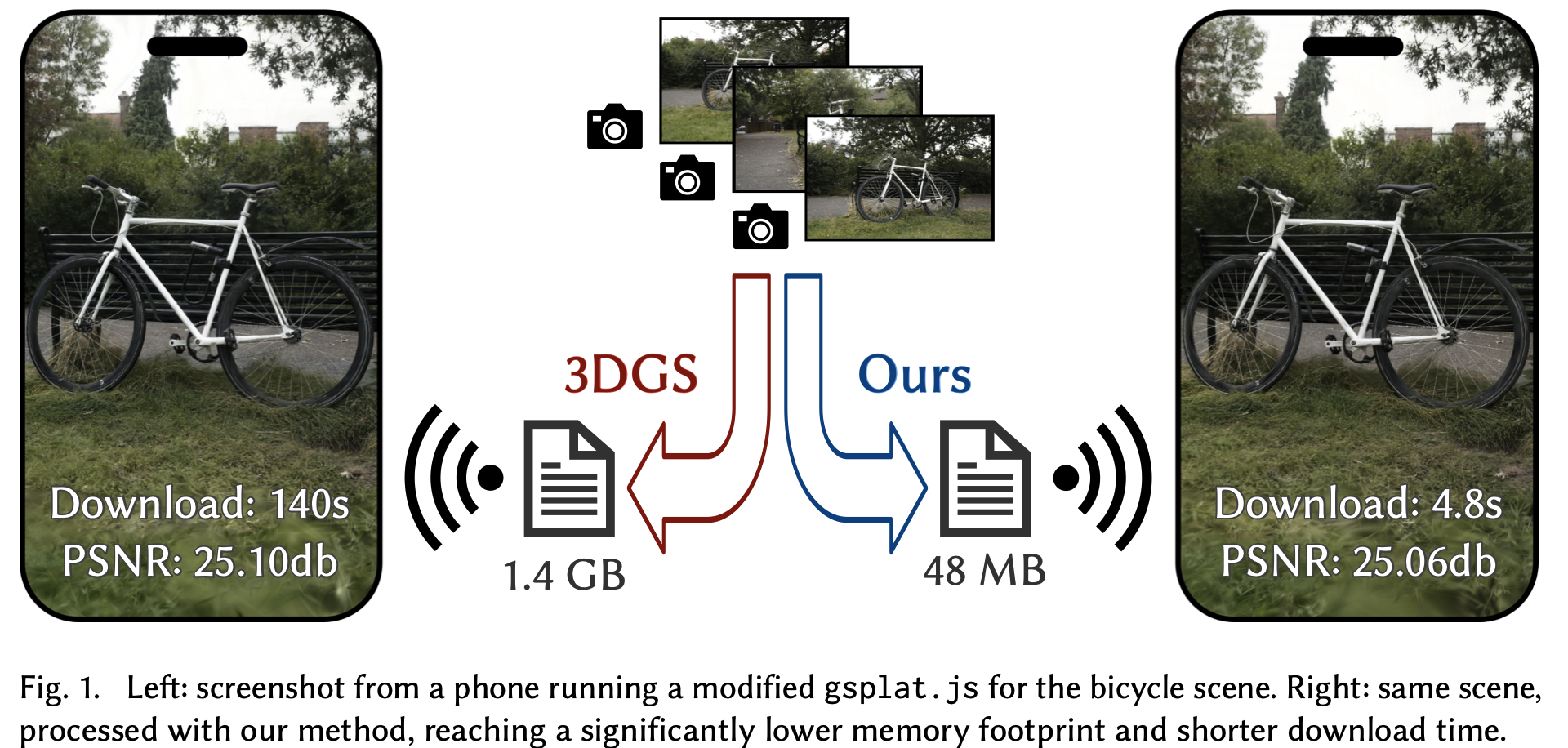
https://repo-sam.inria.fr/fungraph/reduced_3dgs/

https://repo-sam.inria.fr/fungraph/reduced_3dgs/reduced_3DGS_i3d.pdf

瘦身版3DGS：MEMORY REDUCTION FOR 3DGS

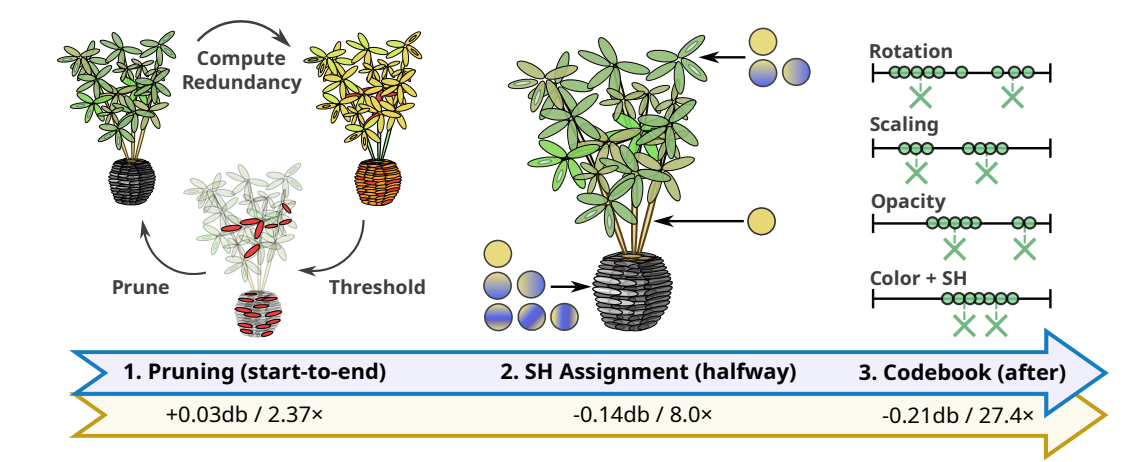
Redundant Primitive Removal

Searching for regions where a large number of primitives exist, but here each of these primitives contributes little to the resulting rendered image.

Ideally, a 3D region around 𝑔 of that extent should be occupied by a low number of primitives

To make this decision for each Gaussian primitive 𝑔 in space, we find the number of other primitives 𝑔′ overlapping a spherical region around 𝑔.

The sphere extent is chosen based on the pixel footprint of the closest view in which 𝑔 is visible (i.e., inside the camera frustum). The closest view corresponds to the smallest pixel footprint \(𝑎_{min}\)

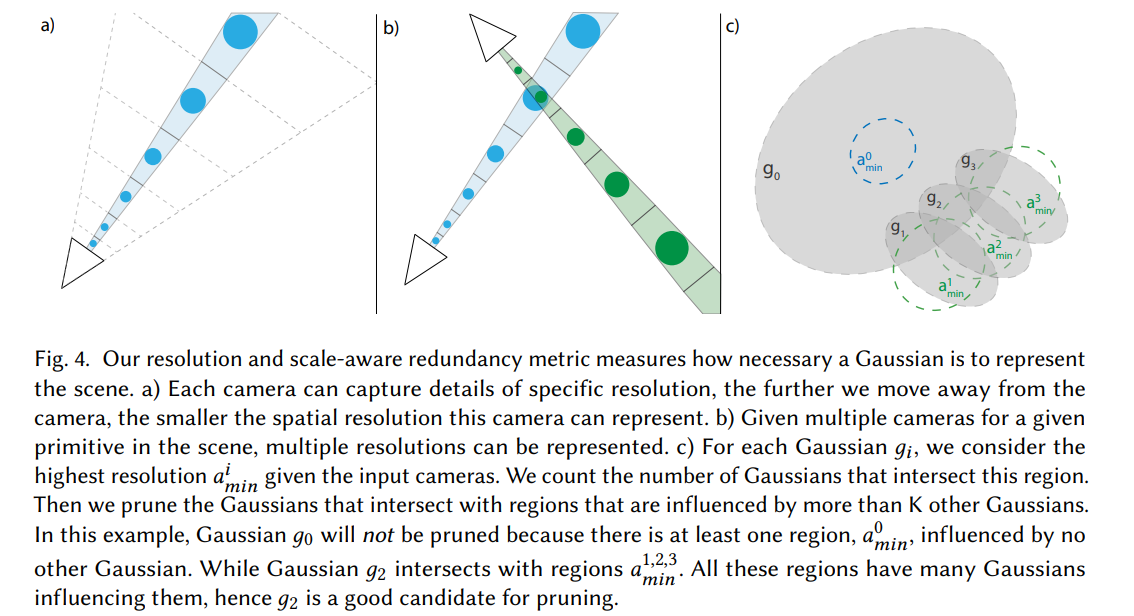
Spatial redundancy score

分数的算法：Counting the number of intersections

加速方式

To limit the number of intersection tests, we first apply a k-NN search with a high number of neighbors (30) on the set of primitives to find candidate intersecting primitives.

删减方式

第一步：Filter

Filter those whose score is greater than an adaptive threshold \(\tau_p = max(\mu + \lambda_r \sigma,3)\)

𝜇 and 𝜎 are the mean and standard deviation of the redundancy score for all primitives
\(\lambda_r = 1\) in all experiments
found that culling primitives with a redundancy score less than 3—i.e., a primitive contributes to at least one region where it coincides with just two other primitives—adversely affects quality.

第二步：Delete filtered primitives

因为each primitive is not independent of other primitives, delete 50% of filtered primitives

delete based on low opacity

第三步：Encourage opacity values to be as low as possible

adding an 𝐿1 sparsity term on opacity to encourage opacity values to be as low as possible.

encourage the creation of lower-contribution primitives and is particularly effective when we cull the bottom 50% of redundant candidate primitives
(optional) remove 3% of lowest opacity primitives each time, with a maximum opacity threshold of 0.05, as removing primitives with larger opacity values degraded the quality.

Adaptive Adjustment of Spherical Harmonics Bands

In many cases, a single RGB color value may suffice

To find the appropriate representation

The first: 纯色

Based on the observation that a primitive that receives the same color from all input views does not need view-dependent effects — determine if the evaluated color of a primitive from all viewpoints has low variance.

如果 have a \(𝜎_𝑐\) lower than a threshold \(𝜖_𝜎\) with the average color \(𝜇_𝑐\), 那就只保留一阶球谐函数 (纯色RGB)(set \(𝜖_𝜎 = 0.04\) in all experiments)

</div>

</div>

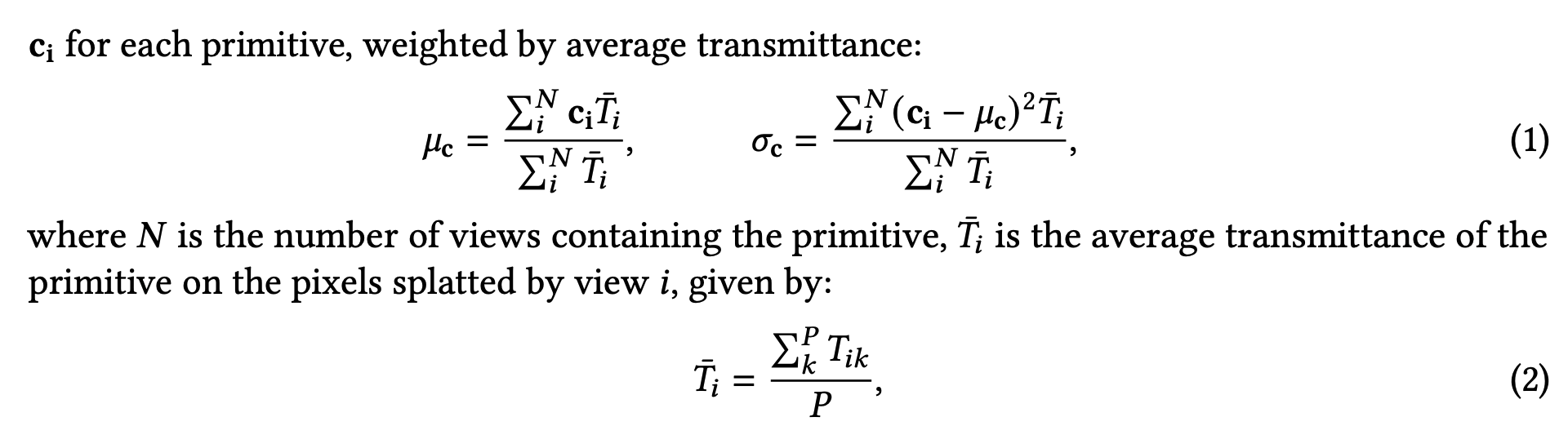
- $$c_i$$ 是不同视角下 primitive观测到的颜色
- 𝑃 is the number of pixels that the primitive is splatted to in view 𝑖
- $$𝑇_{𝑖𝑘}$$ is the transmittance of the primitive for a specific pixel 𝑘

The second: lower band SH coefficients

If the color of a primitive does not change much when evaluated with fewer, lower band SH coefficients, the higher-order ones can be ignored —identify primitives for which dropping the higher-order SH bands creates only a minor change in their evaluated color across all views.

第一步: For every viewpoint, we evaluate the color using only the SH coefficients belonging to the first 𝑞 SH bands for each primitive, resulting in colors \(𝑐_𝑞\), with 𝑞 ∈[0,3]
第二步: calculate the Euclidean distance between the full color \(𝑐_3\) and the remaining three, resulting in three color distances \(𝑑_0\),\(𝑑_1\),\(𝑑_2\).
第三步: Take the average of each distance value across all views, weighted by average transmittance (和上图一样)
第四步: choose the lowest band 𝑞 for which \(𝑑_𝑞\) is below a threshold \(𝜖_{cdist}\) (set to 0.04) and remove the remaining higher bands.
A sparsity loss on SH coefficients. Doing so discourages the use of higher bands

Quantization of the Final Representation

Observation: only limited dynamic range and precision need to be stored for most primitive attributes.

Create a codebook using K-means clustering

Codebook size: 256 entries
- one for opacity,
- one for the three scaling components,
- one for the real part components of quaternion rotation,
- one for the imaginary components of quaternion rotation,
- one for the coefficients of the base color,
- one per 3-channel color component for each of the 15 SH coefficient groups.

Applying 16-bit half-float quantization

For remaining, uncompressed floating point values (i.e., position and codebook entries)

Reduced 3DGS