Score Distillation Sampling (SDS)

DreamFields [Jain et al, CVPR2022], DreamFusion [Poole et al, ICLR2023]

We distill the knowledge learned by a pretrained diffusion model in the form of a score.

To see whether the rendered image from the 3D representation looks realistic or not.

Knowledge Distillation

Use a discriminator to output the conformity (Score)

Use pre-trained image diffusion models instead of CLIP

Leverage a pretrained diffusion model to measure the alignment between the rendered image $x_0$ and the given prompt y

• The loss for the real image $x_0$ will be close to zero; The loss for the fake image $x_0$ will not be close to zero.
• Use the loss function of DDPM or DDIM as the measure of alignment.

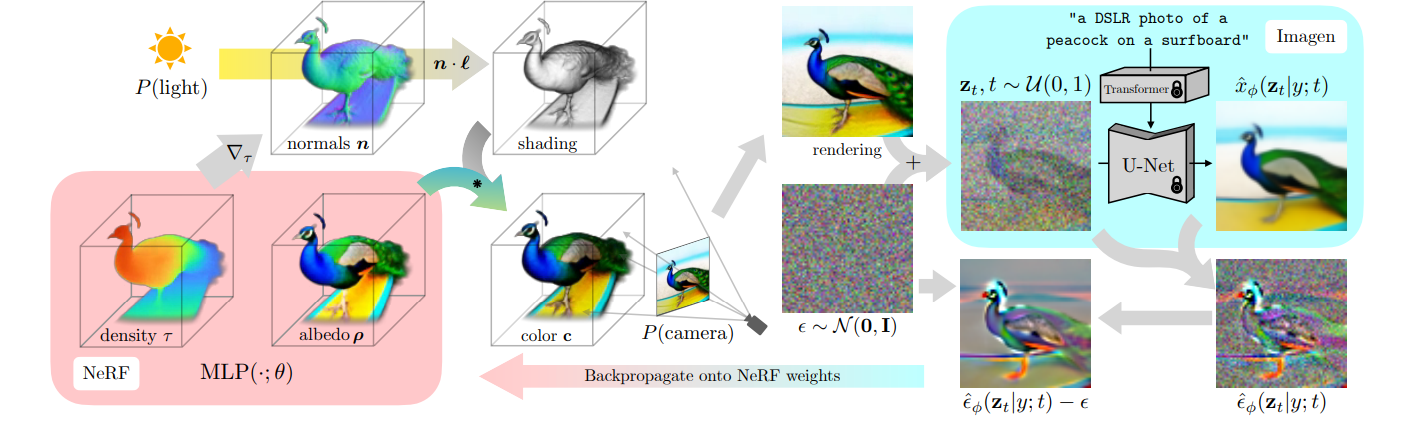
3D Reconstruction via Optimization

\[\nabla_\theta \mathcal{L}_{\text{DF}}(\theta) = \frac{\partial}{\partial \theta} \left\| \hat{\epsilon}_\theta \left( \sqrt{\bar{\alpha}_t} g(\theta; c) + \sqrt{1 - \bar{\alpha}_t} \epsilon_t, y, t \right) - \epsilon_t \right\|^2 \]

1. Render the 3D representation $\theta$ into a specific view c (Can use Nerf)
   • $g(\theta; c)$ → $x_0$ (Rendering image above)
2. Add noise to the rendered image $g(\theta; c)$
   • $\sqrt{\bar{\alpha}_t} g(\theta; c)+ \sqrt{1 - \bar{\alpha}_t} \epsilon_t$ → $x_t$ ($z_t$ above)
3. Predict the noise using the noise predictor.
   • $\hat{\epsilon}_\theta \left( \sqrt{\bar{\alpha}_t} g(\theta; c) + \sqrt{1 - \bar{\alpha}_t} \epsilon_t, y, t \right)$
4. Backpropagate onto $\theta$ while minimizing the $\epsilon_t$ difference (update NeRF weight)

Reducing the computational cost

• Drop the noise predictor Jacobian to save computation time and memory
• The final SDS gradient is thus defined as follows
  • $\nabla_\theta \mathcal{L}{\text{SDS}}(\theta) = \left( \hat{\epsilon}\theta (x_t, y, t) - \epsilon_t \right) \frac{\partial x_t}{\partial \theta}$

Connection between SDS and Denoising Process

Score Distillation via Inversion (SDI)

Using DDIM inversion to calculate unknown $x_t$

In editing, SDS tends to lose the identity of the input image. Delta Denoising Score [Hertz et al,. ICCV 2023]

Posterior Distillation Sampling (PDS)

A modification of SDS for text-driven NeRF editing enables proper geometric and appearance changes without losing the identity of the input image.

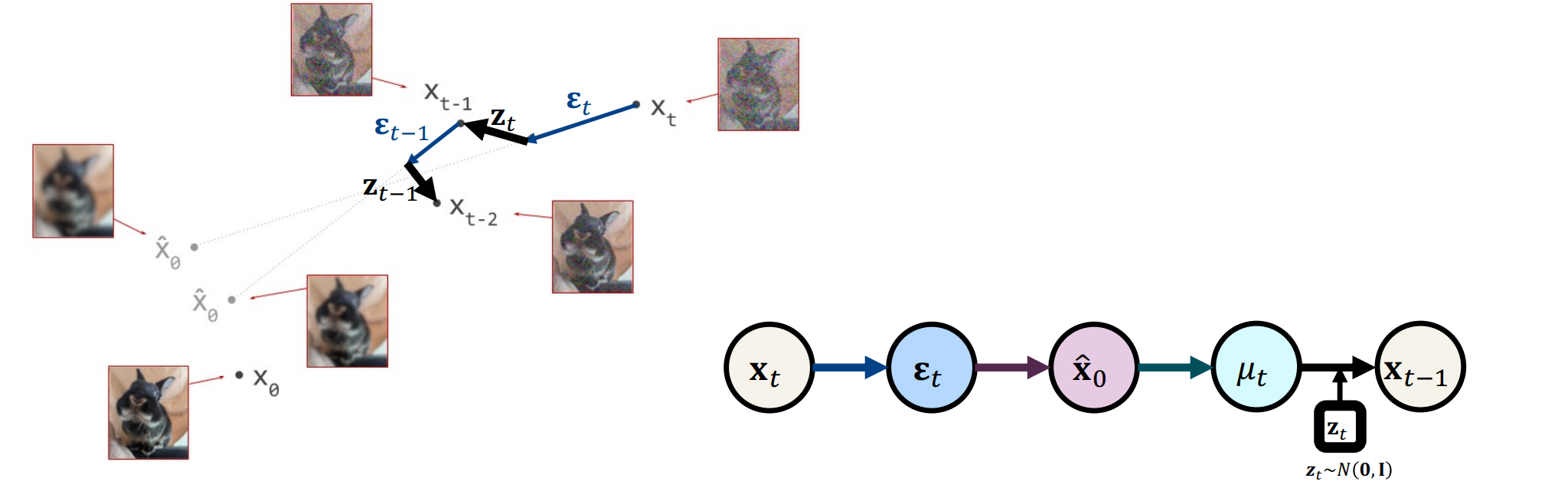
Key Idea: The random noise added to the trajectory $z_t$ at each step encodes identity of the object.

The loss function can be rewritten as follows:

\[\mathcal{L}_{\text{PDS}}(\mathbf{x}_0; \mathbf{x}_0^{\text{ref}}) = \mathbb{E}_{t, \epsilon} \left[ \psi(t) \|\mathbf{x}_0 - \mathbf{x}_0^{\text{ref}}\|_2^2 + \chi(t) \|\hat{\epsilon}_t - \hat{\epsilon}_t^{\text{ref}}\|_2^2 \right]\]

• $\psi(t);\chi(t)$ is the ratio of the time-varying weights of the two terms matters for the quality
• $|\mathbf{x}_0 - \mathbf{x}_0^{\text{ref}}|_2^2$ is identity preservation term
• $|\hat{\epsilon}_t - \hat{\epsilon}_t^{\text{ref}}|_2^2$ is DDS term

Comparative Analysis of Editing Process

• SDS: Collapses to a single point. (Tend to lose the identity of the input image)
• DDS: Strays too far from the $\mathbf{x}_0^{\text{ref}}$ point.
• PDS: Shifts minimally toward the blue distribution.