Attention is All You Need

Positional Encoding

\[PE(pos, 2i) = \sin\left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right) \] \[PE(pos, 2i+1) = \cos\left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right) \]

• pos is the position （time / 单词在句子中的位置 / 时间戳）
• I is the dimension （index in dimension $d_{model}$）

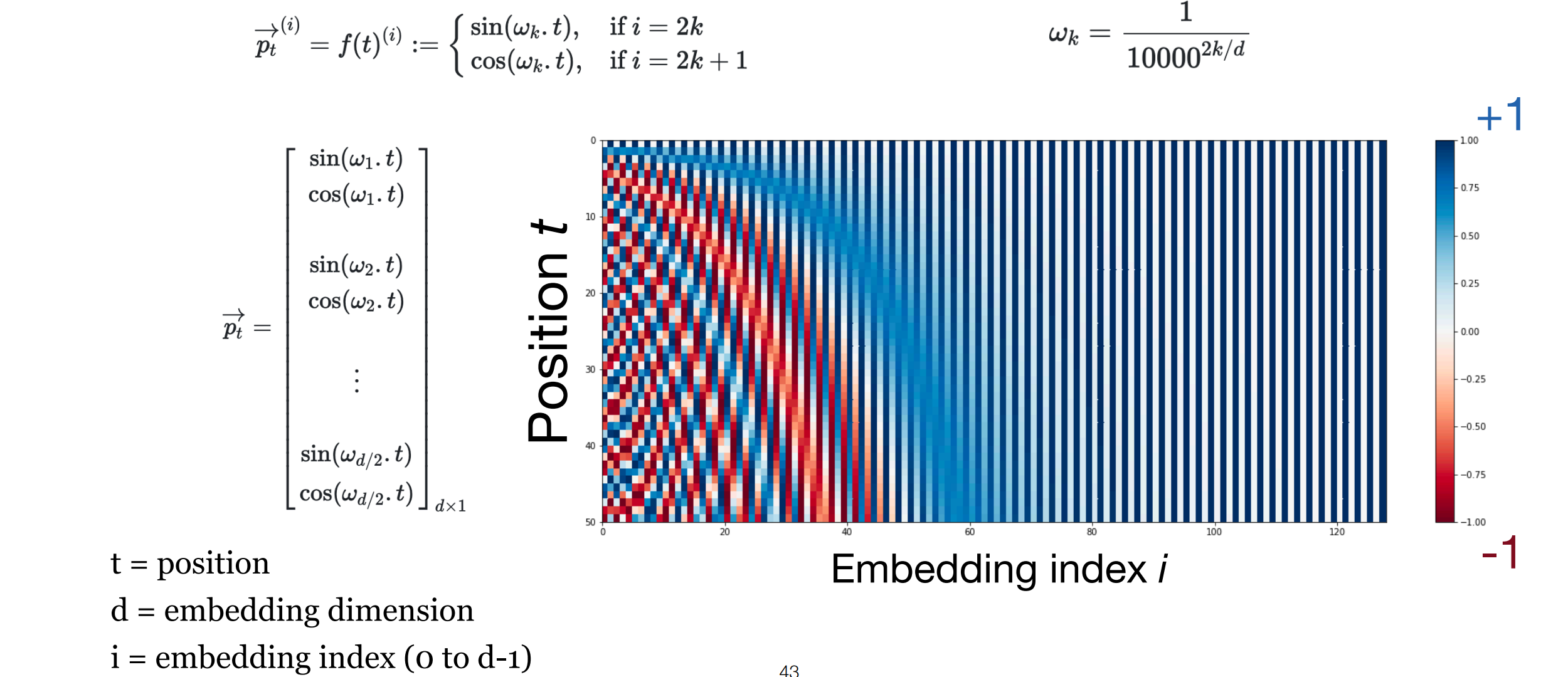
• The positional encodings have the same dimension $d_{model}$ as the embeddings, so the two can be summed.

Attention

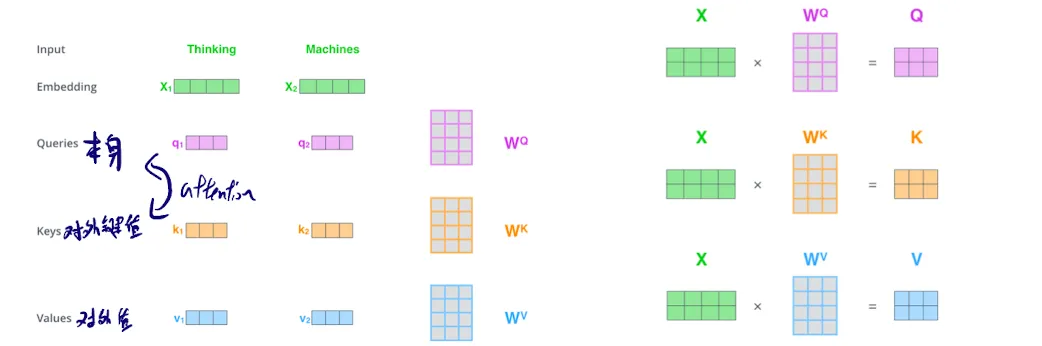
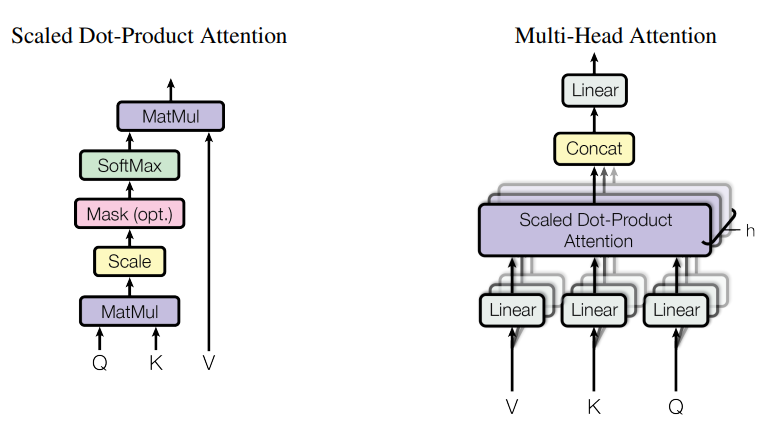
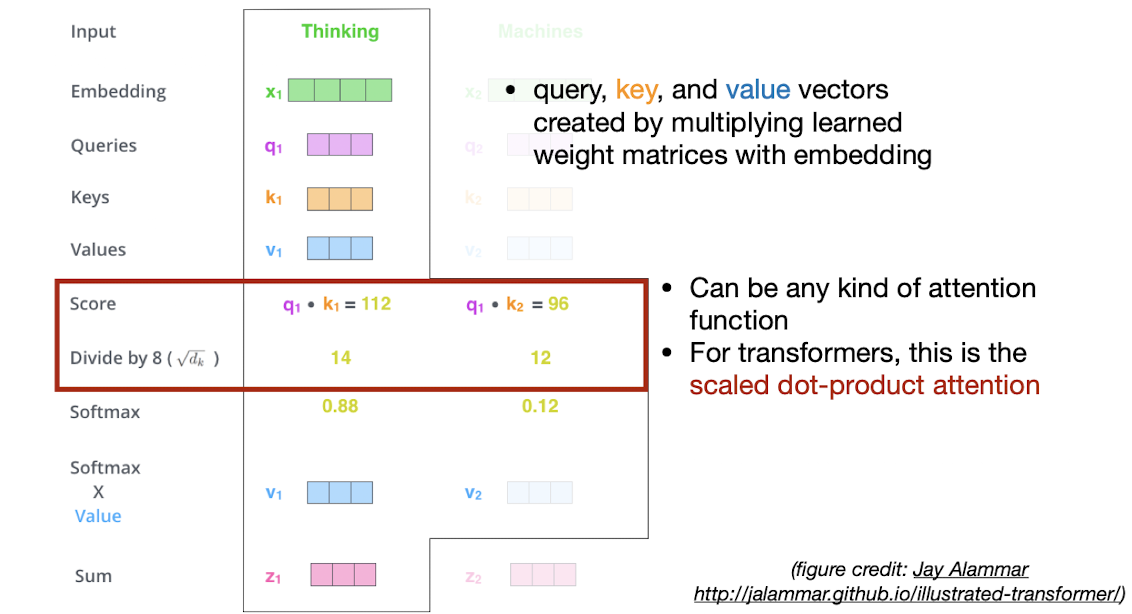
Self-Attention

\[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V \]

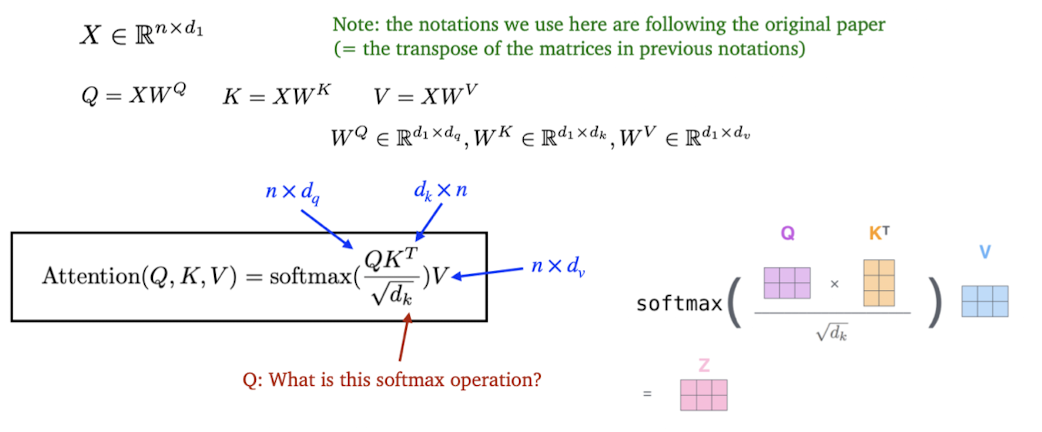
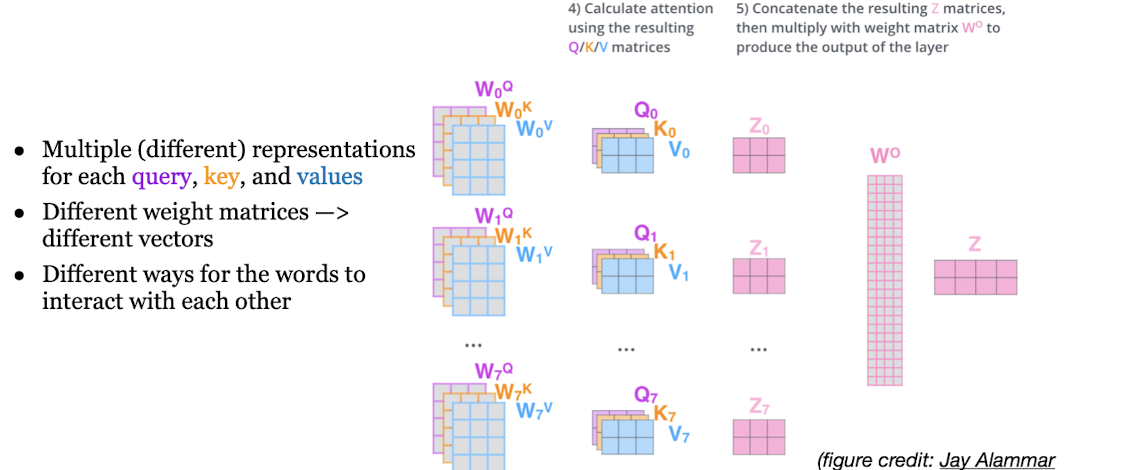
Multi-head Attention

\[\text{MultiHead}(Q, K, V) = \text{Concat}(head_1, \dots, head_h) W_O\] \[\quad \text{where} \quad head_i = \text{Attention}(QW_Q^i, KW_K^i, VW_V^i)\]

The projections are parameter matrices: $\quad W_Q^i \in \mathbb{R}^{d_{model} \times d_k}, \quad W_K^i \in \mathbb{R}^{d_{model} \times d_k}, \quad W_V^i \in \mathbb{R}^{d_{model} \times d_v}, \quad W_O \in \mathbb{R}^{hd_v \times d_{model}}$

Encoder

通过上面描述的 Multi-Head Attention, Feed Forward, Add & Norm 就可以构造出一个 Encoder block， Encoder block 接收输入矩阵 $X_{(n×d)}$ ，并输出一个矩阵 $O_{(n×d)}$。通过多个 Encoder block 叠加就可以组成 Encoder。

第一个 Encoder block 的输入为句子单词的表示向量矩阵，后续 Encoder block 的输入是前一个 Encoder block 的输出，最后一个 Encoder block 输出的矩阵就是编码信息矩阵 C，这一矩阵后续会用到 Decoder 中。

Decoder

第一个 Multi-Head Attention 层

采用了 Masked 操作 因为不允许后出现的词汇影响先出现的词汇。

如果不这么做，后面的词汇可能会提前泄漏接下来内容的线索。

需要确保代表后续Token对前面Token的影响力能够被有效地削弱到0

第二个 Multi-Head Attention 层

根据 Encoder 的输出 C计算得到 K, V，根据上一个 Decoder block 的输出 Z 计算 Q (如果是第一个 Decoder block 则使用输入矩阵 X 进行计算)，后续的计算方法与之前描述的一致。

这样做的好处是在 Decoder 的时候，每一位单词都可以利用到 Encoder 所有单词的信息 (这些信息无需 Mask)。

Softmax

计算下一个单词的概率