变分自编码器（VAE，Variational Autoencoder）

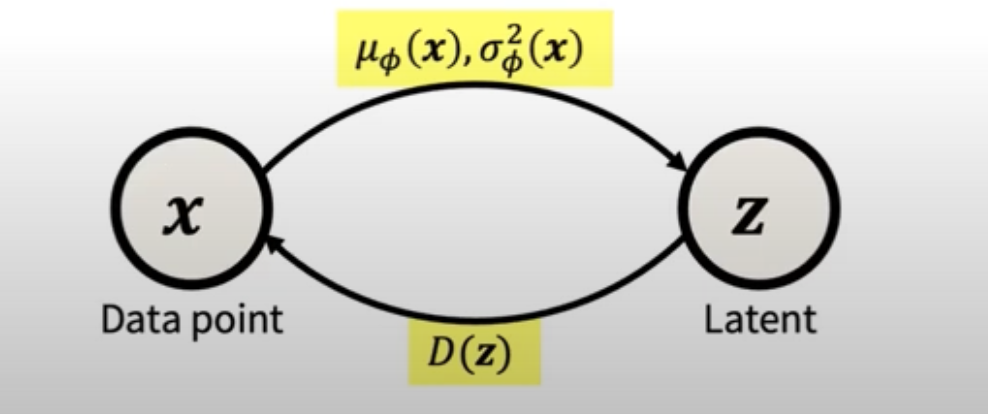
VAE 结构

1. 编码器

通常使用一个神经网络来参数化后验分布 $q(z/x)$，它将输入数据 x 映射到潜在空间 z 的分布，通常是高斯分布，输出均值和方差（或对数方差)。

常见的做法是使用卷积神经网络（CNN) , 输出潜在空间 z 的均值和方差（或对数方差), 这将被用于参数化潜在空间的分布。

class Encoder(nn.Module):
    def __init__(self, latent_dim=64):
        super(Encoder, self).__init__()
        self.conv1 = nn.Conv2d(3, 32, 4, stride=2, padding=1)
        self.conv2 = nn.Conv2d(32, 64, 4, stride=2, padding=1)
        self.conv3 = nn.Conv2d(64, 128, 4, stride=2, padding=1)
        self.fc_mu = nn.Linear(128 * 8 * 8, latent_dim)
        self.fc_logvar = nn.Linear(128 * 8 * 8, latent_dim)

    def forward(self, x):
        x = torch.relu(self.conv1(x))
        x = torch.relu(self.conv2(x))
        x = torch.relu(self.conv3(x))
        x = x.view(x.size(0), -1)  # Flatten the output
        mu = self.fc_mu(x)
        logvar = self.fc_logvar(x)
        return mu, logvar

2. 解码器

也是一个神经网络，它将潜在变量 z 映射回数据空间，用来重建输入数据x。解码器的输出 $q(x/z)$是给定潜在变量 z 的条件概率。

解码器将潜在变量 z 映射回图像空间。通常使用转置卷积（反卷积）来从潜在空间重建输入图像。

class Decoder(nn.Module):
    def __init__(self, latent_dim=64):
        super(Decoder, self).__init__()
        self.fc = nn.Linear(latent_dim, 128 * 8 * 8)
        self.deconv1 = nn.ConvTranspose2d(128, 64, 4, stride=2, padding=1)
        self.deconv2 = nn.ConvTranspose2d(64, 32, 4, stride=2, padding=1)
        self.deconv3 = nn.ConvTranspose2d(32, 3, 4, stride=2, padding=1)

    def forward(self, z):
        x = self.fc(z)
        x = x.view(x.size(0), 128, 8, 8)  # Reshape to a 4D tensor
        x = torch.relu(self.deconv1(x))
        x = torch.relu(self.deconv2(x))
        x = torch.sigmoid(self.deconv3(x))  # Sigmoid to constrain pixel values between [0, 1]
        return x

重参数化技巧（Reparameterization Trick）

在 VAE（变分自编码器）中，直接从后验分布 $q(z/x)$ 中采样是一个不可微的过程，因为采样的结果会受到随机性影响，导致不能计算梯度。为了避免这个问题，我们使用了重参数化技巧，将随机性从分布的参数中提取出来，让采样过程变得可微：

\[z = \mu(x) + \sigma(x) \cdot \epsilon\]

这里：

μ(x) 和 σ(x) 是编码器的输出，分别代表均值和标准差。
$\epsilon \sim \mathcal{N}(0, I)$ 是从标准正态分布中采样的噪声向量，它是固定的、独立于 x 的

通过重参数化技巧，采样 z 不再直接依赖于随机的过程，而是变成了一个确定性过程，其中噪声 ϵ 和网络输出 μ(x) 和 σ(x) 可以一起参与梯度计算。这使得整个过程变得可微，进而可以通过反向传播计算梯度并优化模型。

class VAE(nn.Module):
    def __init__(self, latent_dim=64):
        super(VAE, self).__init__()
        self.encoder = Encoder(latent_dim)
        self.decoder = Decoder(latent_dim)

    def forward(self, x):
        mu, logvar = self.encoder(x)
        z = self.reparameterize(mu, logvar)
        x_reconstructed = self.decoder(z)
        return x_reconstructed, mu, logvar

    def reparameterize(self, mu, logvar):
        # 使用重参数化技巧进行采样
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        z = mu + eps * std
        return z

VAE 的训练目标

VAE 的目标是最大化数据的对数似然p(x)，但是由于直接优化对数似然是不可行的，VAE通过优化变分下界(ELBO）来近似真实的对数似然。(Loss = Reconstruction Loss + KL Divergence)

\[\mathcal{L}_{\text{VAE}}(x) = \mathbb{E}_{q(z|x)}[\log p(x|z)] - \text{KL}(q(z|x) \| p(z))\]

x: input
z: latent varible
先验p(z), 设为标准正态分布 $\mathcal{N}(0, I)$。
- 重构损失（Reconstruction Loss）： 确保生成的数据尽可能接近原始输入数据。
- KL 散度（Kullback-Leibler Divergence）： 强制潜在变量的分布接近预设的先验分布（通常是标准正态分布）。

\[\text{KL}(\mathcal{N}(\mu, \sigma^2) \| \mathcal{N}(0, 1)) = \frac{1}{2} \left( \mu^2 + \sigma^2 - \log \sigma^2 - 1 \right)\] \[\text{KL}(q(z|x) \| p(z)) = \frac{1}{2} \left( \mu^2(x) + \sigma^2(x) - \log \sigma^2(x) - 1 \right)\]

def vae_loss(x, x_reconstructed, mu, logvar):
    # 重建损失：使用二元交叉熵损失（适用于图像像素值在[0, 1]之间）
    reconstruction_loss = nn.functional.binary_cross_entropy(x_reconstructed.view(-1, 3 * 64 * 64), x.view(-1, 3 * 64 * 64), reduction='sum')
    
    # KL 散度
    kl_loss = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
    
    # 总损失
    total_loss = reconstruction_loss + kl_loss
    return total_loss

在 VAE 中，编码器输出的是潜在变量 z 的均值（mu）和对数方差（logvar）

Advanced VAE

β-VAE

变分自动编码器（VAE）的一个扩展版本，通过引入一个可控参数β，在重构损失和潜在表示的分布正则化之间引入平衡，促进解耦表示的学习。

β-VAE 引入了一个可调参数 $\beta > 0$ 来控制 KL 散度的权重，从而在重构和解耦性之间取得平衡：

\[\mathcal{L}_{\text{VAE}}(x) = \mathbb{E}_{q(z|x)}[\log p(x|z)] - \beta * \text{KL}(q(z|x) \| p(z))\]

当 β=1 时，β-VAE 退化为标准 VAE。
当 β>1 时，模型更注重约束潜在变量分布，倾向于学习更加解耦的潜在表示。
如果 β<1，重构质量会更高，但可能牺牲潜在变量的独立性。

FactorVAE

VAE，虽然可以生成高质量的样本，但潜在空间中的表示往往是纠缠的（entangled），即潜在变量之间存在复杂的依赖关系。FactorVAE 通过鼓励潜在变量的统计独立性

FactorVAE 的关键在于优化目标函数中增加了一个额外的解耦正则项，称为 total correlation (TC)。

\[\mathcal{L}_{\text{FactorVAE}} = \mathcal{L}_{\text{VAE}} + \gamma \cdot \text{TC}\] \[\text{TC}(z) = \text{KL}(q(z) \,||\, \prod_j q(z_j))\]

为了计算 TC，FactorVAE 引入了一个称为discriminator（判别器）的网络。判别器用于区分来自联合分布q(z) 和独立分布 $\prod_{j} q(z_j)$的样本。通过训练判别器估计 TC，并在生成器的优化过程中将 TC 作为一个惩罚项加入目标函数。

简单地将编码器输出 z 按照维度索引分解为 $z_1, z_2, \dots, z_d$
打乱联合样本 z 的维度，例如对 z 的每一维 $z_j$ 独立地随机重排，形成新的样本 z′。

判别器网络的输入是z 和 z′，输出一个概率，表示输入样本是否来自 q(z)。