Autoregressive Modeling to Images via Next-Token Prediction

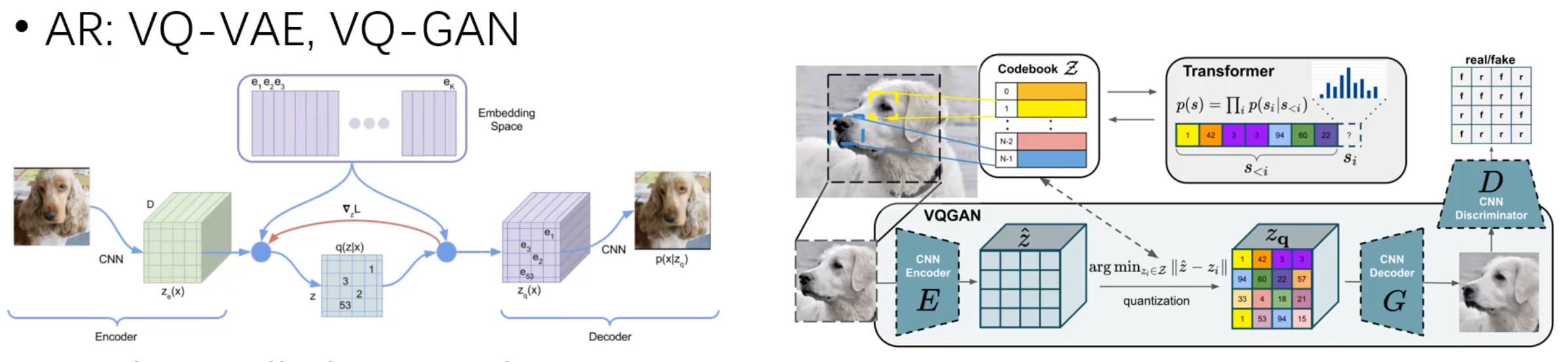
1. 图像离散化：从连续到离散的转换

首先，要将图像从一个二维连续信号表示为离散 tokens，常用 量化自动编码器 (Quantized AutoEncoder)。以下是具体过程：

(1) 编码阶段：生成特征图

图像 $I \in \mathbb{R}^{H \times W \times 3}$ b输入到编码器网络（通常是卷积神经网络，CNN），生成一个低分辨率的特征图:$f \in \mathbb{R}^{h \times w \times C}$

(2) 特征量化：离散化特征

通过一个可学习的代码本 (Codebook)将特征 f 转换为离散 tokens：

\[q_{i,j} = \underset{k}{\arg\min} \, \|f_{i,j} - e_k\|^2, \quad e_k \in \mathbb{R}^C\]

• $q_{i,j} \in \{1, 2, \dots, V\}$ 表示特征位置(i,j) 被量化后的离散索引，V 是代码本的大小。
• $\|f_{i,j} - e_k\|^2$：特征向量 $f_{i,j}$ 与代码本向量 $e_k$ 的欧几里得距离平方。
• $e_k \in \mathbb{R}^C$：代码本向量 $e_k$ 是 C-维空间中的第 k 个嵌入向量, 可以写作$\text{lookup}(\mathbf{Z}, \mathbf{k})$。

量化后，特征图 $f \in \mathbb{R}^{h \times w \times C}$转换为离散索引图：$q \in [V]^{h \times w}$

(3) 解码阶段：重构图像

为了评估量化的质量，量化后的 tokens 可以通过解码器（通常也是 CNN）还原为原始图像：

$\hat{\mathbf{f}} = \text{lookup}(\mathbf{Z}, \mathbf{q})$, $\hat{\mathbf{I}} = D(\hat{\mathbf{f}})$ 解码器从离散 tokens q 中学习生成与原图像尽可能接近的重建结果。

\[L = \| \mathbf{I} - \hat{\mathbf{I}} \|_2^2 + \| \mathbf{f} - \hat{\mathbf{f}} \|_2^2 + \lambda_P L_P(\hat{\mathbf{I}}) + \lambda_G L_G(\hat{\mathbf{I}})\]

2. 1D 顺序定义：为自回归建模排序

在自回归模型中，需要定义 token 的一维顺序。常见策略包括：

(1) 扫描顺序

将 2D tokens 按照预定义规则排列为一维序列 $q’ \in [V]^{h \cdot w}$. 常见扫描方式：

• 行优先顺序
• 列优先顺序
• Zigzag 顺序: 交替排列，减少局部依赖的破坏。

(2) 位置编码

为每个 token 添加位置信息，例如通过一个可学习的位置嵌入 $p_{i,j}$ 这样，每个 token $q_{i,j}$ 被表示为：

\[z_{i,j} = q_{i,j} + p_{i,j}\]

实现流程

• 图像编码：通过编码器生成特征图。
• 特征量化：使用代码本将连续特征量化为离散索引。
• 定义顺序：按预定义规则将离散 tokens 排列为一维序列。
• 位置编码：嵌入位置信息以加强空间感知。
• 自回归建模：对生成的 1D 序列进行下一个 token 的预测。