Reference: https://www.cs.sfu.ca/~haoz/teaching/cmpt464/index.html SFU CMPT 464 Computer Graphics Course Notes by Hao Zhang 学习笔记 可能有理解错的地方，不保真!!!

3D Shape Representations: Implicit Functions, Parametric Reps, and Fitting

Curves

Implicit representations

Shape = \(\{x \in R^k / f(x) = 0\}\)

• Inside-outside function
  • Plane: \(f(x) = n* (x-p)\)
  • Sphere \(f(x) = (x-c)^2 -r^2\)
  • inside f(x) < 0; outside f(x) > 0

Parametric representations

parametric cubic curves and surfaces

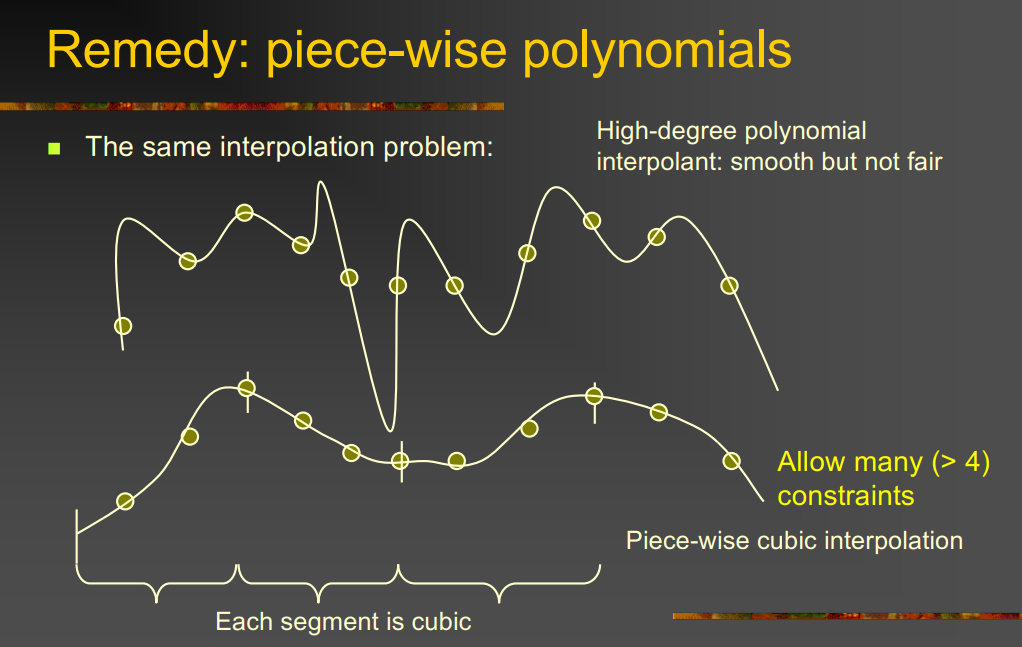
Parametric cubic segment

\(z(t)=c_3t^3+c_2t^2+c_1t+c_0,t∈[0,1]\) In matrix form: \(\mathbf{x}(t) = \begin{bmatrix} t^3 & t^2 & t & 1 \end{bmatrix} \begin{bmatrix} a_3 \\[2mm] a_2 \\[1mm] a_1 \\[1mm] a_0 \end{bmatrix} = TA\)

• T is said to be the monomial basis

但是现实中在曲线设计语境下不太直观

通常在 CAD 或图形学里，人们更倾向于用端点 + 切向量 (Hermite) 或者控制点 (Bézier)来设计曲线，没有办法直接指定\(a_3, a_2, a_1, a_0\)

• P1, P2, P3, and P4 serve as control points
• b是 basis polynomials

Derivatives and Continuity

• f(x) 在 x=a 连续 满足条件
  • f(a) 存在
  • 极限\(\lim_{x \to a} f(x)\) 存在
  • \[\lim_{x \to a} f(x) = f(a)\]
• 导数
  • 一阶导数 → 切线方向（曲线走向）
  • 二阶导数 → 弯曲程度（加速度、曲率）

• Parametric continuity of a curve (smoothness of motion)(平滑程度):

  当你有多段曲线拼接在一起时（比如 Bézier 段、样条段），你希望它们在连接点处“平滑”地过渡传说中的Continuity of piecewise curves

  “Visual” smoothness:

  • C0 continuous: curve is connected
  • C1: requires C0 and 1st-order derivative is continuous
  • C2: requires C1 and 2nd-order derivative is continuous
  • Cn: requires Cn – 1 and n-th derivative continuous
• Geometric continuity similar with Cn
  • G0: 曲线段在连接点处相交（位置相同）和C0一样
  • G1: 满足 G0，且1阶导数在连接处成比例 (proportional): \(p′(1)=k*q′(0)\)
    • 两条曲线在连接点的切线方向相同，但导数大小可以不同
  • G2: 满足 G1，且2阶导数在连接处成比例 (proportional)

Curvature of plane curve

弯曲得有多厉害 κ（kappa）

\(\kappa = \left| \frac{d\mathbf{\theta}}{ds} \right| = \frac{|x'(t)y''(t) - y'(t)x''(t)|}{\big((x'(t))^2 + (y'(t))^2\big)^{3/2}}\)

• θ is the turning angle and s is arc length
• 密切圆（osculating circle），这个圆在该点处“最好地逼近”曲线
  • 有相同的一阶导 (切线方向相同); 有相同的二阶导 (弯曲程度相同)
  • 也可以写成 \(\kappa = 1/R\), 但是每个点的 osculating circle 半径 R

Cubic Hermite curves

2个点 + 2个tangents

• \[h_{00}(t) = 2t^3 - 3t^2 + 1, h_{10}(t) = t^3 - 2t^2 + t, h_{01}(t) = -2t^3 + 3t^2, h_{11}(t) = t^3 - t^2\]
  • \(h_{00}, h_{01}\) 控制端点位置
  • \(h_{10}, h_{11}\) 控制端点切向量

• Hermite change-of-basis matrix 就是中间那个
• Any cubic parametric curve can be specified in Hermite form

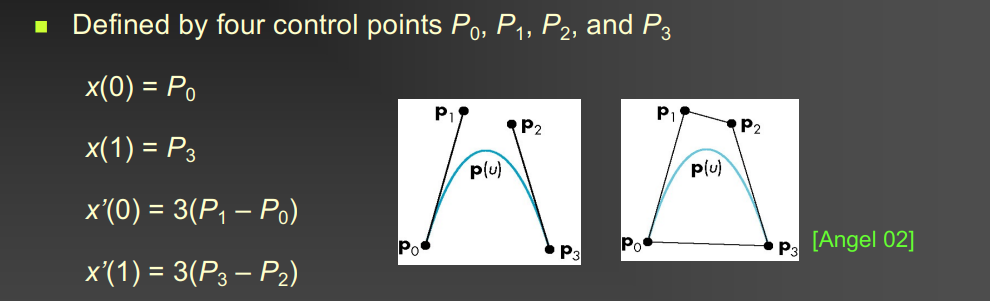
Cubic Bézier curve

由 4 个控制点定义

• \[\begin{aligned} b_1(t) &= (1-t)^3, \\ b_2(t) &= 3(1-t)^2 t, \\ b_3(t) &= 3(1-t) t^2, \\ b_4(t) &= t^3. \end{aligned}\]
• \[\mathbf{P}(t) = \begin{bmatrix} t^3 & t^2 & t & 1 \end{bmatrix} \begin{bmatrix} -1 & 3 & -3 & 1 \\ 3 & 6 & 3 & 0 \\ -3 & 3 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} \mathbf{P}_0 \\[2mm] \mathbf{P}_1 \\[1mm] \mathbf{P}_2 \\[1mm] \mathbf{P}_3 \end{bmatrix}\]

Convex Hull Property

Bézier 曲线位于由其控制点形成的凸包内, 如果满足:

• \[0 \le b_i(t) \le 1, \quad i=1,2,3,4, \quad \forall t \in [0,1],\]
• \[\sum_{i=1}^4 b_i(t) = 1, \quad \forall t \in [0,1].\]

Bézier basis functions

三次 Bézier 曲线用 4 个控制点→ degree 3 →如果是五次或十次 Bézier 曲线 → 控制点更多

• \[B_i^n(t) = \binom{n}{i} \, t^i (1-t)^{n-i}, \quad i = 0,1,\dots,n\]
  • \[\binom{n}{i} = \frac{n!}{i!(n-i)!}\]
• \[B_i^n(t) = (1-t) B_i^{n-1}(t) + t \, B_{i-1}^{n-1}(t), \quad i=0,1,\dots,n\]
  • \[B_{-1}^{n-1}(t) = B_n^{n-1}(t) = 0\]
• \[\sum_{i=0}^{n} B_i^n(t) = (t + (1-t))^n = 1, \quad t \in [0,1]\]
  • 符合Convex Hull Property: Partition of unity

de Casteljau’s algorithm

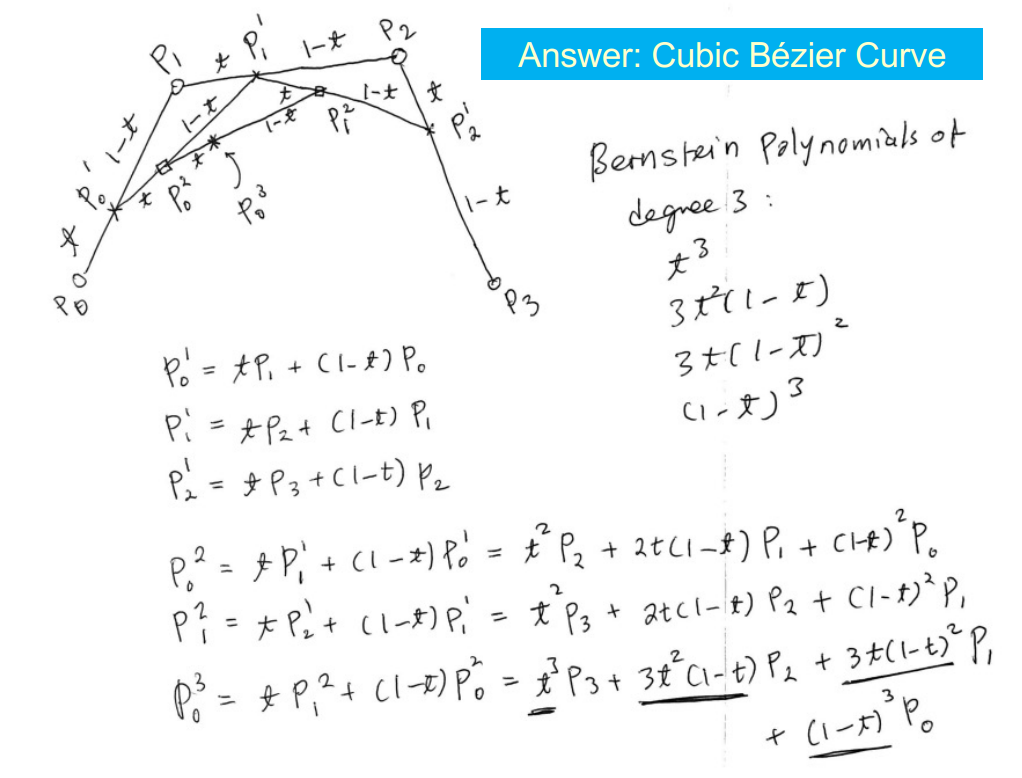
用线性插值逐步逼近 Bézier 曲线上某一点（可以顺便得到曲线在 t 处分割后的控制点）比直接用 Bernstein 多项式更安全，用来实际计算 Bézier 曲线上的点或分割曲线

• 第一步：初始化
  • \[P_i^{(0)} = P_i, \quad i = 0, \dots, n\]
• 第二步：递归差值，每上一层点原来越少，越来越靠近答案
  • \[P_i^{(r)} = (1-t) P_i^{(r-1)} + t P_{i+1}^{(r-1)}, \quad i = 0, \dots, n-r\]
• 第三部：直到减少到1个点为止，得到最终在t处曲线点
  • \(P(t) = P_0^{(n)}\)

    Cubic B-spline curve

由 4 个控制点定义

Two consecutive segments share three control points

m control points → m – 3 segments

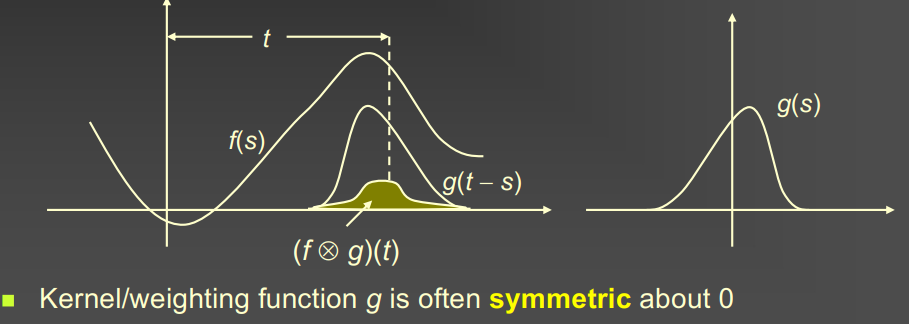
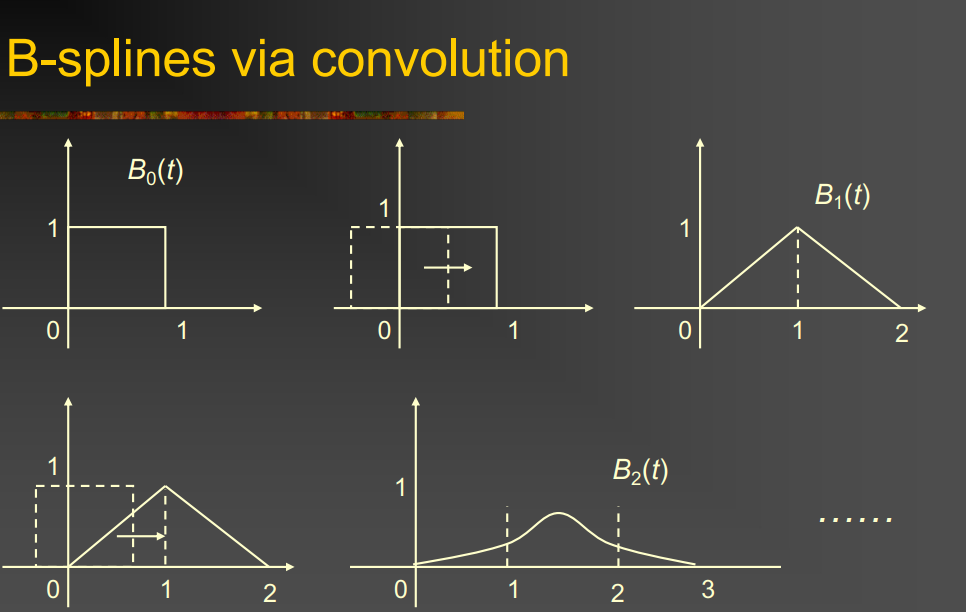
In uniform case (uniform B-splines), B-spline basis can be defined via repeated convolution

$B_l(t) = (B_{l-1} \otimes B_0)(t) = \int B_{l-1}(s) \, B_0(t-s) \, ds$

• Convolution: $(f \otimes g)(t) = \int_{-\infty}^{\infty} f(s)g(t-s)ds$

Surfaces

Tensor-product (TP) surfaces

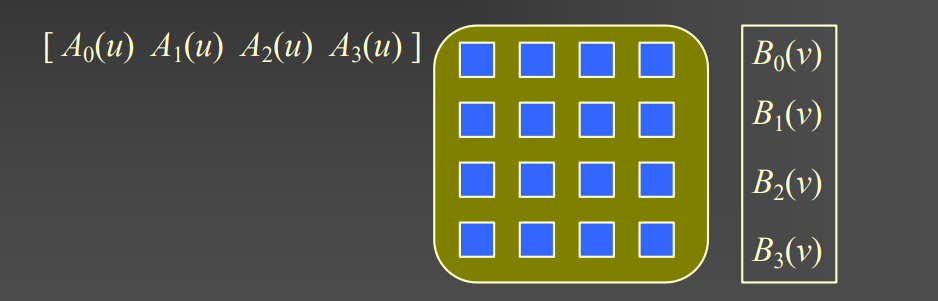
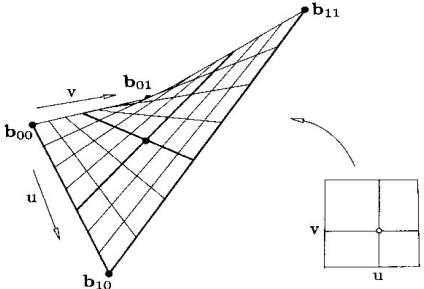
• 第一步 先沿着一个方向 (i.e. u) 造出曲线
  • \[p(u) = \sum_{i=0}^{m} a_i A_i(u)\]
  • 这里的 p(u) 只是参数化的一条曲线，每个 u 对应一个点。
• 控制点沿 v 方向变化, $a_i$ 不再是固定的点，而表示成一个沿 v 方向变化的曲线。
  • \[a_i = q_i(v) = \sum_{j=0}^{n} P_{ij} B_j(v)\]
  • 沿 u 的曲线 p(u) 不再固定，而是随着 v 变化而变化 → 这就形成了无数条曲线（沿 u 方向）堆叠起来生成曲面。
• 最终张量积曲面
  • \[p(u,v) = \sum_{i=0}^{m} \sum_{j=0}^{n} P_{ij} A_i(u) B_j(v) = A(u)^T P B(v)\]
  • 把1，2步结合起来了
  • Surface is controlled by the grid of control points $P_{ij}$
  • A,B 都是基函数

TP cubic 应用

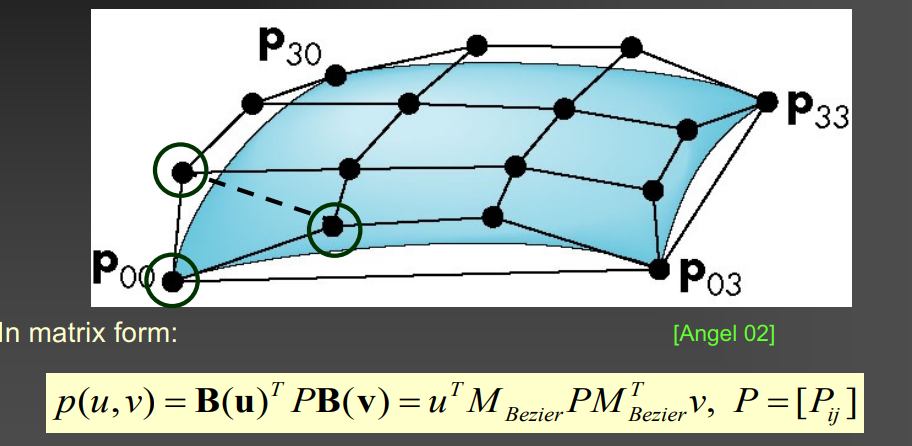
• TP cubic Bézier patch
  • \[p(u,v) = \sum_{i=0}^{3} \sum_{j=0}^{3} P_{ij} B^3_i(u) B^3_j(v) = B(u)^T P B(v)\]
  • Partition of unity: convex hull of 16 control points
  • Four corner vertices are interpolated
  • 角点的切平面由 角点 + uv方向的两个邻近控制点 决定
  • Smoothness of Bézier surface: C1, G1

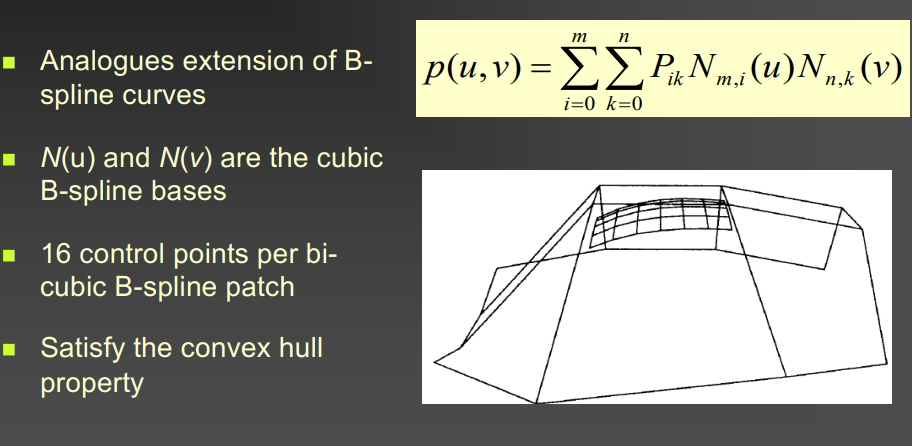
• TP cubic B-splines
  • \[\bm{p}(u,v) = \sum_{i=0}^{m} \sum_{j=0}^{n} \bm{P}_{ij} N^m_i(u) N^n_j(v) = \bm{N}(u)^T \bm{P} \bm{N}(v)\]
  • Smoothness of Bézier surface: C2

Curvature of surfaces

• 规则点（regular point）和 切平面（tangent plane）
  • 该点P 的曲线有无限多条，每条曲线在点P 有一个切向量
  • 如果所有切向量都位于同一个平面内，这个平面就是切平面，点就是规则点
• 曲面法向量（surface normal）是垂直于切平面的向量
• 法截面（normal section）
  • 在曲面上某点P, 取一个包含法向量的平面, 把它切过曲面, 平面与曲面的交线就是法截面
  • 有无数种, **因为你可以绕着法向量旋转平面, 每个平面与曲面的交线就是一条不同的法截面曲线, 每条法截面曲线在点 P 都有自己的曲率
• Principal curvatures: \(\kappa_1 = \max(\kappa_{\text{normal section}}), \quad \kappa_2 = \min(\kappa_{\text{normal section}})\)
  • Gaussian curvature（高斯曲率）\(K = \kappa_1 * \kappa_2\) 反映曲面在一点的整体弯曲性质(方向无关)
    • 曲面局部像马鞍 K < 0
    • 曲面局部像碗 K > 0
    • 曲面局部像平面 K = 0
  • Mean curvature（平均曲率） \(H = \frac{\kappa_1 + \kappa_2}{2}\) 反映曲面在一点的平均弯曲程度(方向无关)
    • H = 0 → minimal surface 最小曲面
  • For a regular point, the two principal (curvature) directions are perpendicular

## Primitive fitting Given a set of points, find the parameters of a primitive (e.g., a line or plane, a sphere, or a cylinder) to provide the best fitting ### Least square (LSQ) Find the primitive which minimizes the sum of squared distances from the set of points - 问题： outliers: Even very few outliers can cause problems

### RANSAC Classify points into inliers, outliers, and eliminate the latter: model/primitive is only fit to the inliers

Meshes and Subdivision

曲线细分（subdivision）

Bézier curve via de Casteljau

如果想要一条 Bézier 曲线的任意子段，也必须用一组新的控制点来表示：方便递归细分、渲染和理论分析 → Multi-resolution

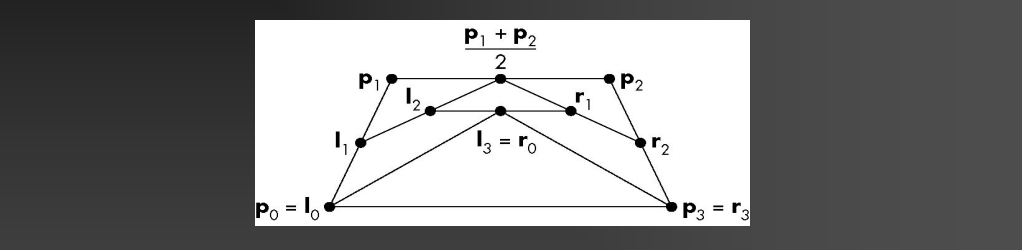
Each set of new control points control half of the Bezier curve

B-Splines through subvidision

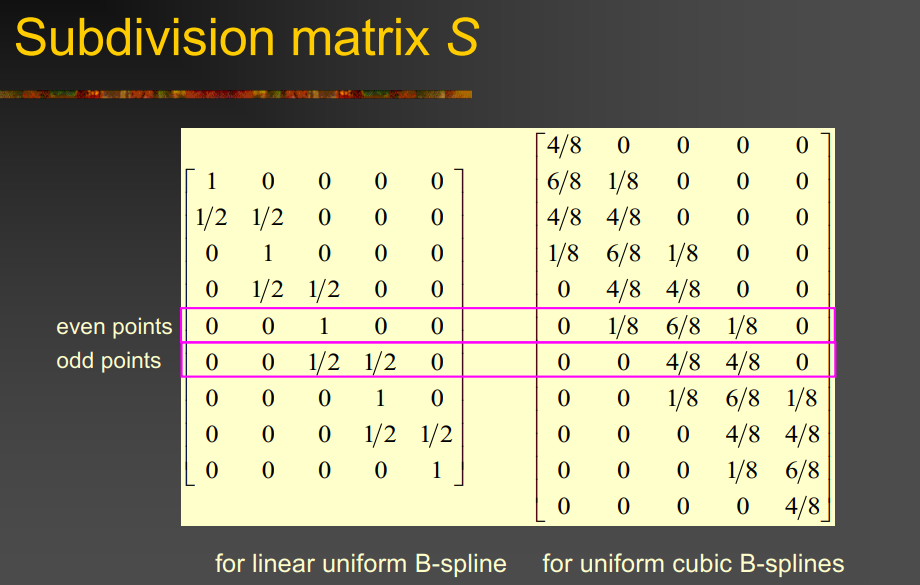
• S is the subdivision matrix
• \(p’ = S p\) is the new, refined set of control points 增长了两倍的新点
• B(2t) represent refined B-spline basis functions

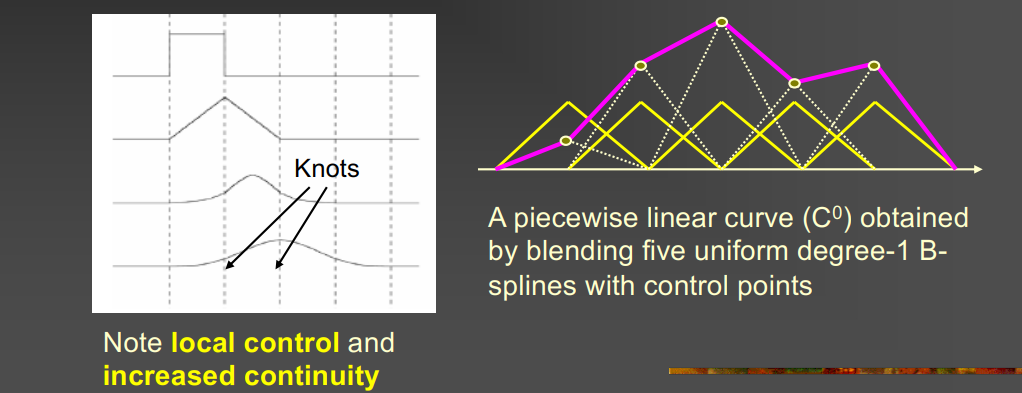
Spline curve is defined by a knot sequence → polynomial pieces join

• Uniform knot spacing
  • Uniform B-spline 可以写成自身的线性组合，满足自相似性质（refinement equation）
    • 你画一条线条的波浪，比如山脉轮廓
    • 如果把它缩小一半，然后平移几次，把几段小山脊叠加起来，你会发现整体看起来和原来的波浪形状一样
    • 自相似：局部缩小+移动+组合 → 恢复整体
  • \[N_k(t) = \sum_{i} h_i \, N_k(2t - i)\]
  • 这是 B-spline 与 subdivision 关联的关键
• Nonuniform knot spacing or repeated knots are also possible

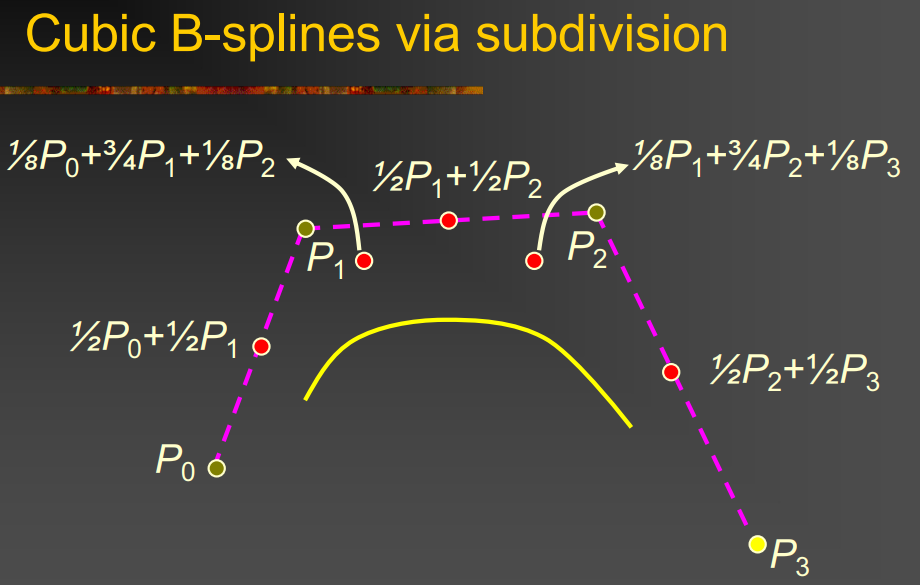
B-splines satisfy the refinement equation: 局部缩小+移动+组合 → 恢复整体 \(B_{l}(t) = \frac{1}{2^{l}} \sum_{k=0}^{l+1} \binom{l+1}{k} * B_{l}(2t - k)\)

那么新的点就可以通过 $p’ = Sp$ 得到：

Meshes / Surface Subdivision

Polygonal mesh → Triangles

Efficient storage: triangle strips → For n triangles in a strip, only need n+2 vertices

Two aspects

• Topological rule: where to insert new vertices? Are old vertices kept?
• Geometrical rule: spatial location of the new vertices – typically given as an average of nearby new or old vertices

Catmull-Clark

• 拓扑规则（Topological rules）
  • 每个面（face）生成一个新的面点（face point）；每条边生成一个新的边点（edge point）；保留旧顶点（old vertex），但暂不移动位置
  • 每个 face point 与该面所有相邻的 edge points 相连；每个旧顶点 与它相邻的 edge points 相连

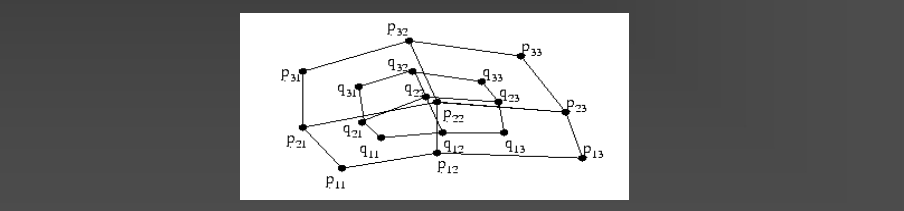
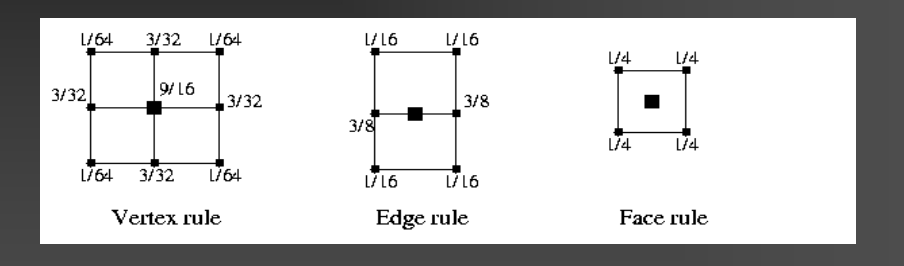
• 几何规则（Geometric rules）
  • 面点（Face point） = 当前面的所有顶点的平均
  • 边点（Edge point） = 当前边两端顶点 + 相邻面点的平均
  • 旧顶点（Vertex point） = 根据周围面点、边点和原顶点加权平均更新位置

• Extraordinary vertices
  • 顶点相邻面数 不是 4（例如 3 个或 5 个）
• Catmull-Clark and B-splines
  • Number of extraordinary vertices never increase
  • Continuity at extraordinary vertices: C1
  • Even if original mesh has faces other than quadrilaterals, after one subdivision, all faces become quadrilaterals

Important properties — Eigen of subdivision matrix

对S做特征分解（Eigen Decomposition）

• \[S \mathbf{x}_i = \lambda_i \mathbf{x}_i, \quad i = 0, 1, \ldots, n-1\]
  • xi 是第 i 个特征向量（eigenvector）
  • λi 是对应的特征值（eigenvalue）
• 我们可以把任意控制点分布 p 用它们来表示
  • \[p=Xa=[x_0,x_1,…,x_{n−1}]a\]
  • \[S^k \mathbf{p} = S^k X \mathbf{a} = X \Lambda^k \mathbf{a}\]
    • \[\Lambda = \mathrm{diag}(\lambda_0, \lambda_1, \ldots)\]
    • 得出 \(S^k \mathbf{p} = \sum_i a_i \lambda_i^k \mathbf{x}_i\)
• 话又说回来
  • x0：整体平移（位置方向）
  • x1,x2：形状变化（切线/曲率方向）
  • 其余 λ₃, λ₄ 更小，对应高阶变化，很快衰减。

Affine invariance

如果你对曲线或曲面的控制点进行仿射变换（平移、旋转、缩放或剪切），通过细分得到的新曲线/曲面就是变换后的形状

• 只需要对控制点做变换，不需要对整个曲线/曲面做复杂运算

Related to the row sum of the subdivision matrix → 矩阵每行加起来“恰好等于 1” → 主特征值eigenvalues为 1 → 极限点存在 = 一定存在的单点，迭代无限次后，新生成点聚集的位置

• Subdivision: \(v = S u, \quad S \in \mathbb{R}^{n \times m}\)
• Affine transform: \(p \mapsto A p + b\)
• 两种方式达到目的：
  • Subdivide then affine: \(v \mapsto (A(Su)^T + b 1_n^T)^T = S u A^T + 1_n b^T\)
  • Affine then subdivide: \(v \mapsto S(A u^T + b 1_m^T)^T = S u A^T + S 1_m b^T\)
• 两种方案等价的条件: \(S 1_m = 1_n \quad \text{(unit row sum = 1)}\)

Smoothness

Related to eigenvalues of the subdivision matrix

• 次大特征值（次主特征值）决定了曲线/曲面的平滑程度。
• 如果次特征值小于 1，曲线/曲面就会光滑收敛。
• 其他次特征值对应的特征向量表示控制点在局部 neighborhood 中的波动模式

Point Cloud & Mesh

Voxels

Embed 3D shape in a regular volumetric grid

IM-Net: trained on voxel inputs

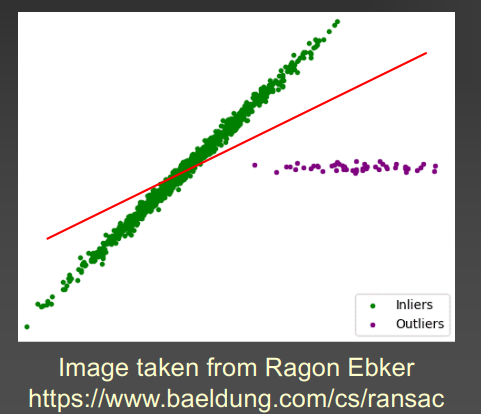
Point-based representation (PBR)

用 一组三维点 (points) 来表示一个 3D 表面，而不是用网格 (triangles, polygons) 或体素 (voxels)

• 没有明确的连接关系
  • 需要通过 k 最近邻 (kNN) 来局部建立邻域关系
    • 找到某个点最近的 10 个点，用它们估计该点所在曲面的方向或曲率或法线。

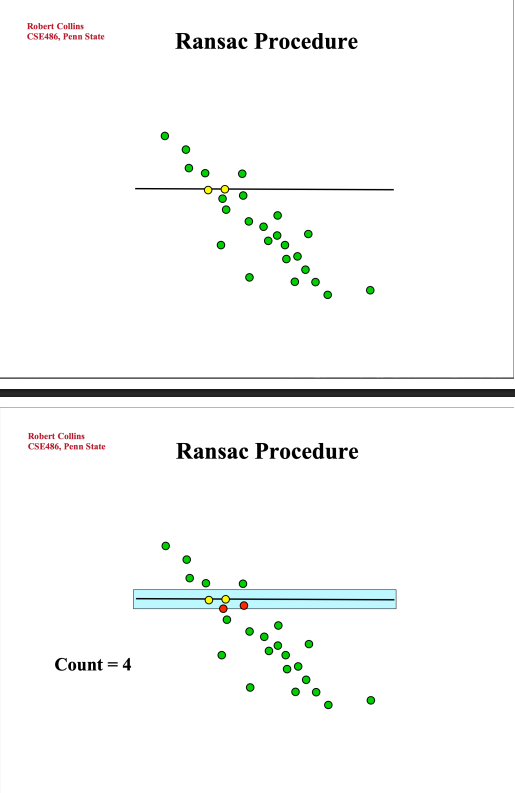
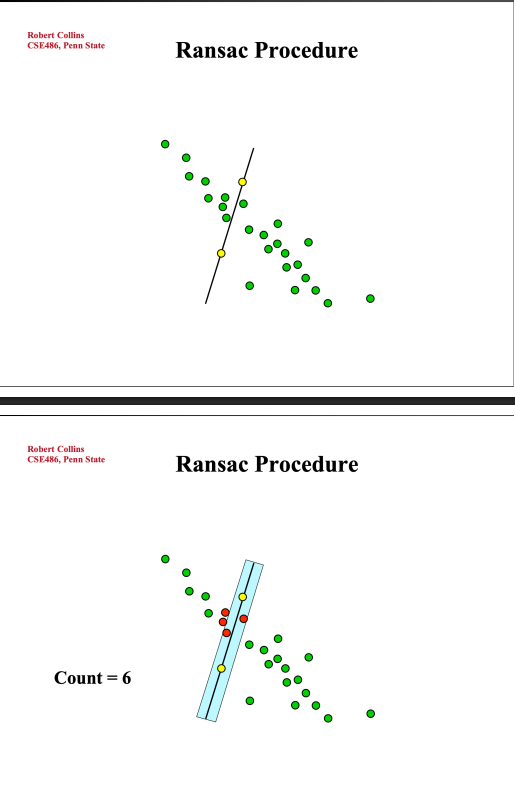
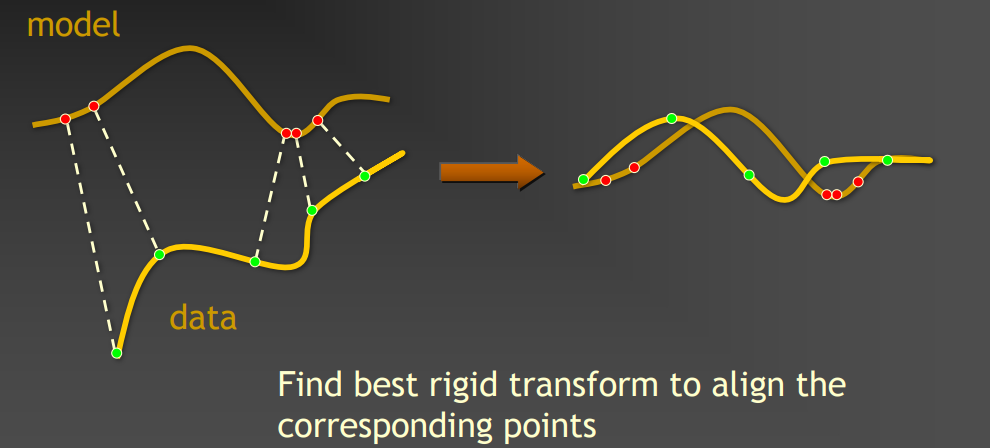
Iterative closest point (ICP) algorithm

• Input: data and model shapes
• Objective:
  • Rigid transform = rotation + translation
  • Minimize mean squared error from data points to closest points in model

def compute_centroid(points):
    return np.mean(points, axis=0)

def icp_point_to_point(source, target, max_iterations=100, tolerance=1e-4):
    """
    Point-to-Point ICP algorithm with correct visualization transforms.
    """
    tree = KDTree(target)
    source_transformed = source.copy()
		record = np.eye(4)
    all_transforms = [record.copy()]
		prev_error = np.inf

    for i in range(max_iterations):
        # Find the nearest neighbors of the source points in the target point cloud.
        distance, indices = tree.query(source_transformed)
        threshold = np.percentile(distance, 95)
        mask = distance <= threshold
        source_filtered = source_transformed[mask]
        target_matched = target[indices][mask]

        source_center = compute_centroid(source_filtered)
        target_center = compute_centroid(target_matched)

        # Demean the source and target points.
        src_demean = source_filtered - source_center
        tgt_demean = target_matched - target_center

        # Compute the covariance matrix between the source and target points.
        covariance = src_demean.T @ tgt_demean
        U, _, Vt = np.linalg.svd(covariance)
        # Compute the rotation matrix R & translation vector t
        R = Vt.T @ U.T
        if np.linalg.det(R) < 0:
            Vt[2, :] *= -1
            R = Vt.T @ U.T
        t = target_center - R @ source_center

        # Compute the transformation matrix
        T = np.eye(4)
        T[:3, :3] = R
        T[:3, 3] = t

        record = T @ record
        all_transforms.append(record.copy())

        # Update the source points using the computed rotation matrix and translation vector.
        source_transformed = (R @ source_transformed.T).T + t

        # Compute the error as the mean of the distances between the source and target points.
        error = np.mean(distance[mask])
        if np.abs(prev_error - error) < tolerance:
            break
        prev_error = error

    print(f"ICP converged after {i+1} iterations, final error = {error:.6f}")
    return source_transformed, error, all_transforms